Hans Walser, [20230215]

Steiner-Kette

Anregung: Anton Gfrerrer, Graz

1 Ein schlechtes Beispiel

Wir beginnen mit zwei ungleichen grünen Kreisen, von denen der eine ganz im Innern des anderen liegt (Abb. 1).

Abb. 1: Zwei ineinander liegende Kreise

Wir passen an einer beliebigen Stelle einen weiteren Kreis ein (Abb. 2.1).

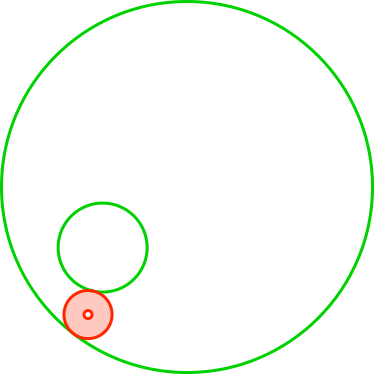
Abb. 2.1: Einpassen eines roten Kreises

Nun fügen wir einen weiteren roten Kreis ein, der die beiden grünen Kreise und den roten berührt (Abb. 2.2).

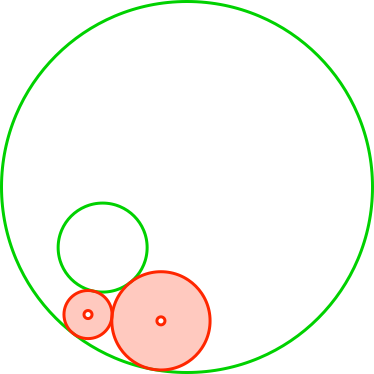
Abb. 2.2: Zweiter roter Kreis

Entsprechend fahren wir fort (Abb. 2.3 bis 2.7).

Abb. 2.3: Dritter roter Kreis

Abb. 2.4: Vierter Kreis

Abb. 2.5: Fünfter Kreis

Abb. 2.6: Sechster Kreis

Abb. 2.7: Der siebente Kreis überlappt den ersten

Wir sehen, dass es nicht aufgeht. Der letzte rote Kreis überlappt teilweise den ersten.

2 Besserer Startkreis?

Vielleicht kommen wir hin, wenn wir den ersten Kreis anders wählen?

Das geht leider nicht, wie die Abbildung 3 illustriert.

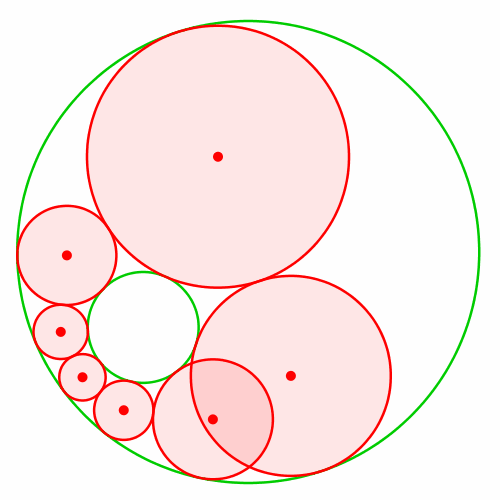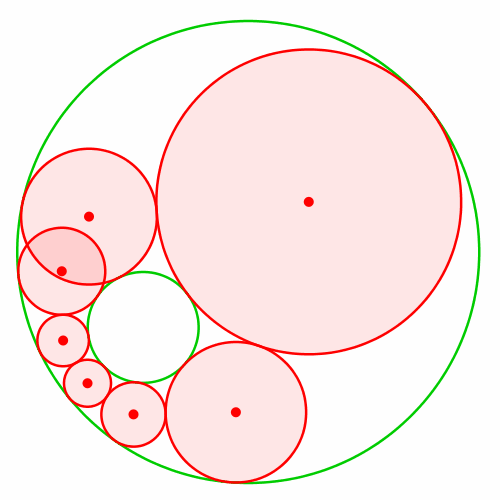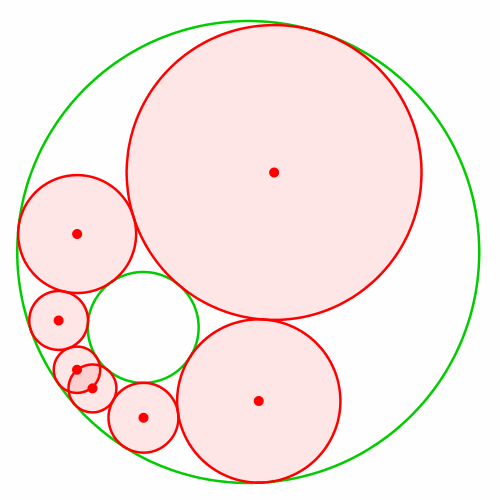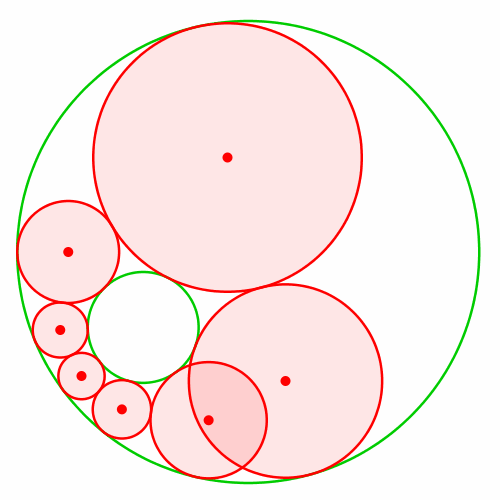
Abb. 3: Verändern des Startkreises hilft nicht

3 Besseres Beispiel

Die Abbildung 4 zeigt ein leicht verändertes Beispiel mit einem ersten Kreis.

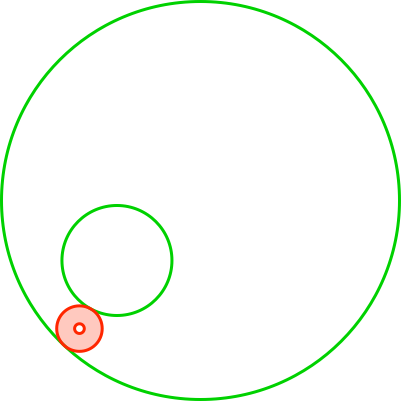
Abb. 4: Verändertes Beispiel

Das Einfügen weiterer Kreis führt zu einer Schließungsfigur (Abb. 5). Es geht auf.

Abb. 5: Schließungsfigur. Steiner-Kette

Eine solche Figur wird als Steiner-Kette bezeichnet.

4 Porismus

Auch jede andere Wahl des Startkreises führt zu einer Schließungsfigur (Abb. 6).

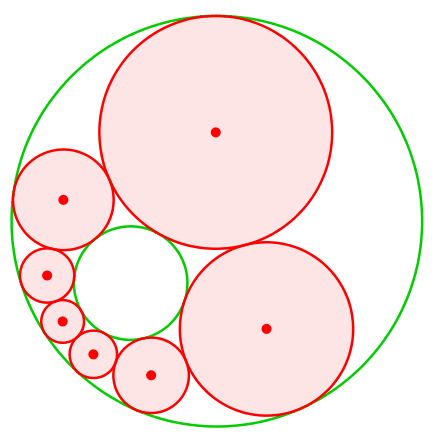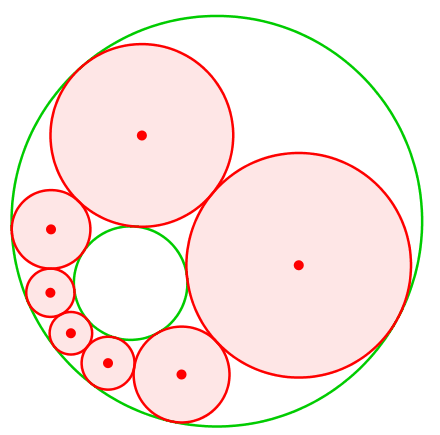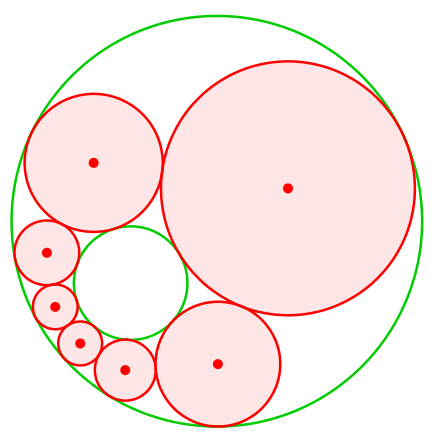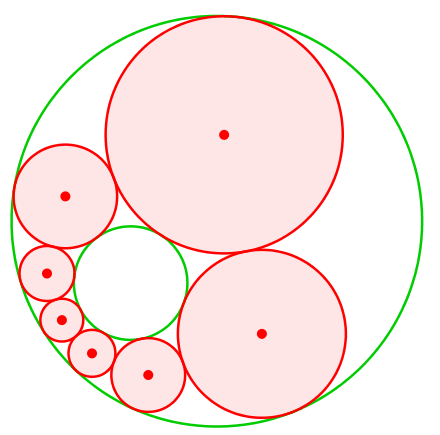
Abb. 6: Einmal Schließungsfigur, immer Schließungsfigur

Eine Eigenschaft, die unabhängig von der Startfigur gilt, heißt Porismus.

5 Konstruktion einer Steiner-Kette

Wir ordnen m rote Kreise ringförmig an (Abb. 7 für m = 7). Innen und außen zeichnen wir je einen grünen Begrenzungskreis. Das ist der einfachste Fall einer Steiner-Kette.

Abb. 7: Kreise im Ring

Natürlich können wir die roten Kreise problemlos verdrehen.

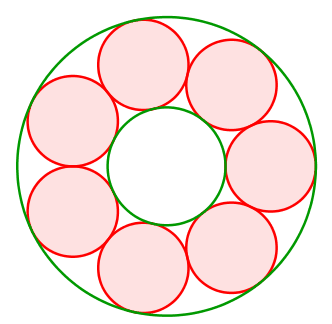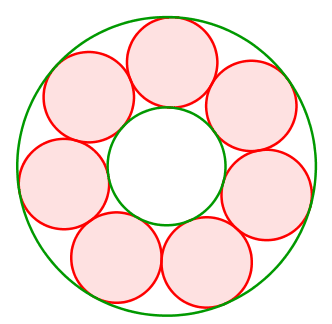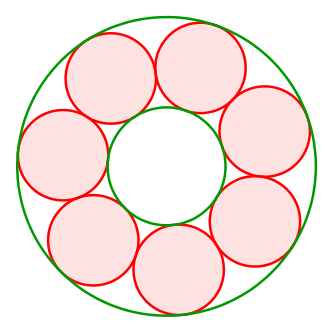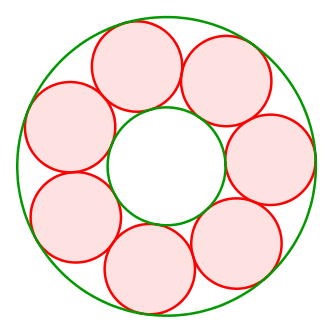
Abb. 8: Drehen der Kreise

Mit einer Kreisspiegelung können wir den Sonderfall auf einen allgemeinen Fall abbilden (Abb. 9).

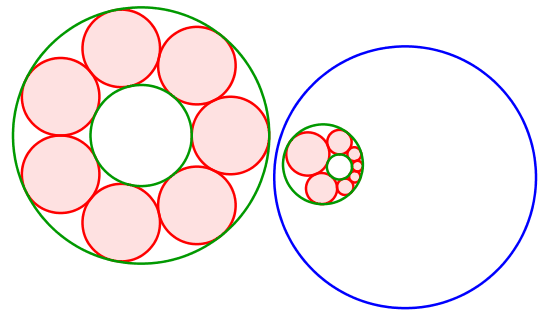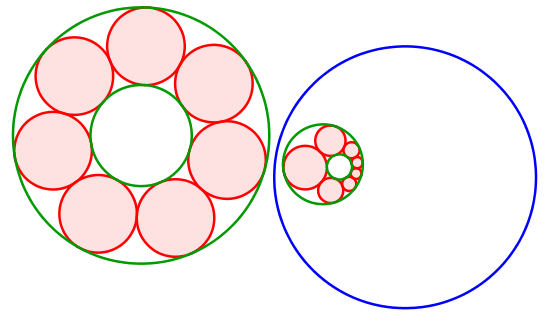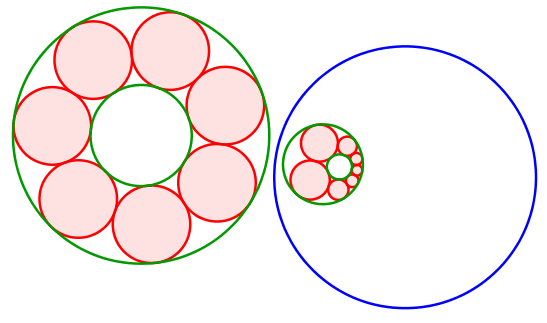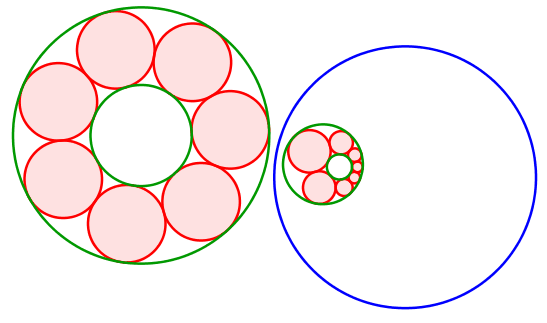
Abb. 9: Kreisspiegelung

6 Anmerkungen

Je nach Wahl des Spiegelkreises sieht die Steinerkette unterschiedlich aus. Die Mittelpunkte der roten Kreise der Steinerkette bewegen sich auf einem Kegelschnitt. Nachweis mit Abstandsdefinitionen der Kegelschnitte.

6.1 Grüne Kreise ineinander. Elliptischer Fall

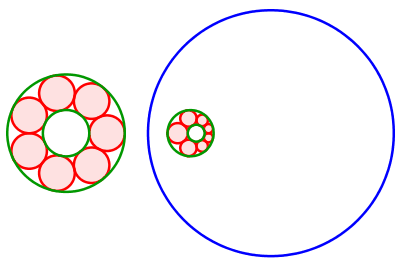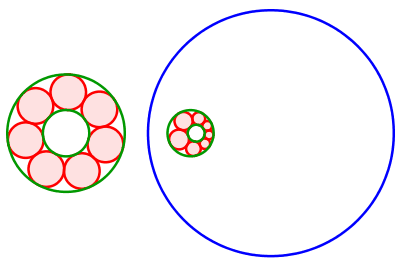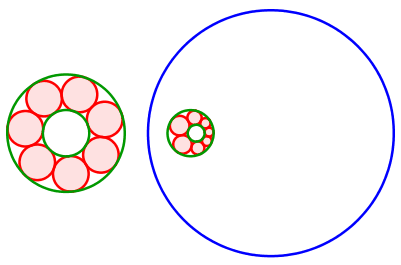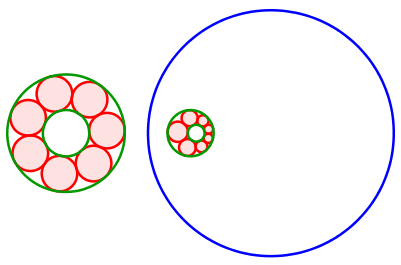
Abb. 10: Die grünen Randkreise liegen ineinander

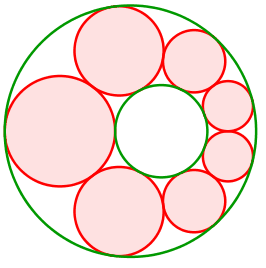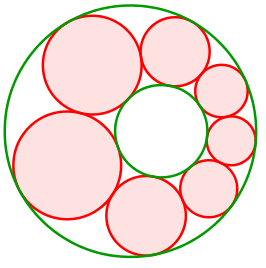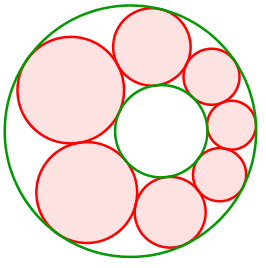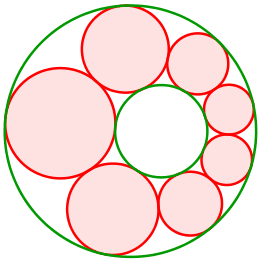
Abb. 11: Die grünen Randkreise liegen ineinander

Die Mittelpunkte der roten Kreise bewegen sich auf einer Ellipse. Diese hat die Mittelpunkte der grünen Kreise als Brennpunkte.

6.2 Grüne Kreise nebeneinander. Hyperbolischer Fall

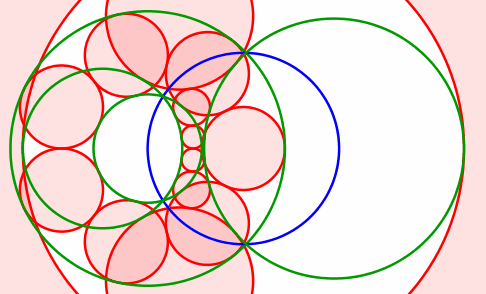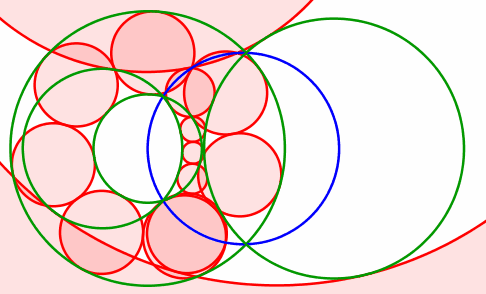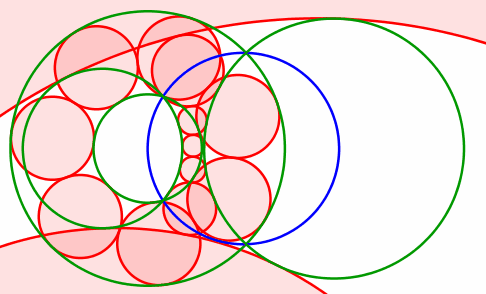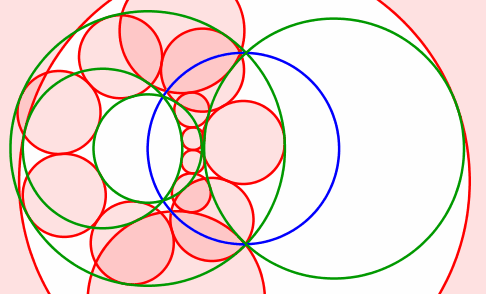
Abb. 12: Grüne Kreise nebeneinander

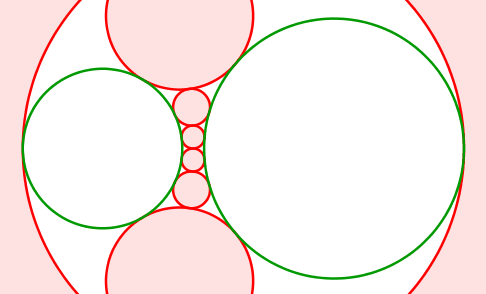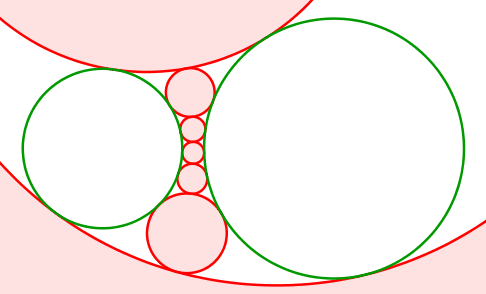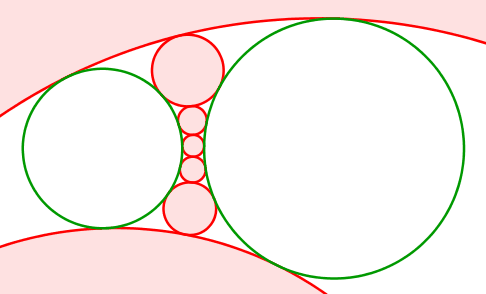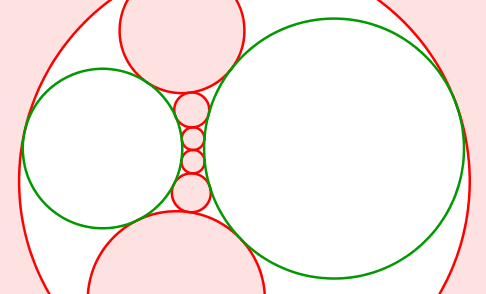
Abb. 13: Grüne Kreise nebeneinander

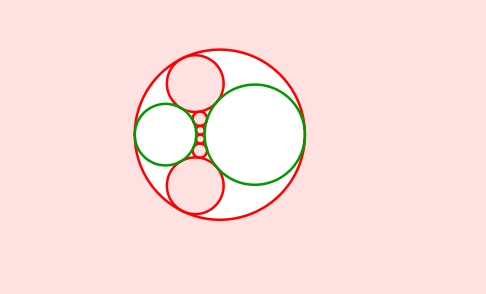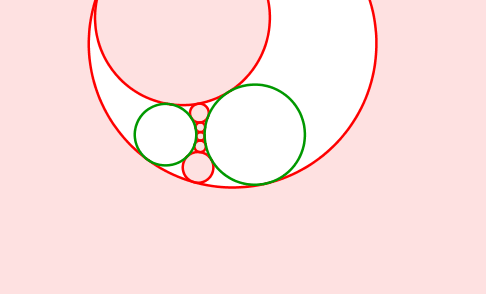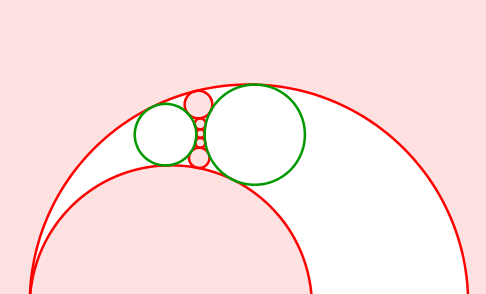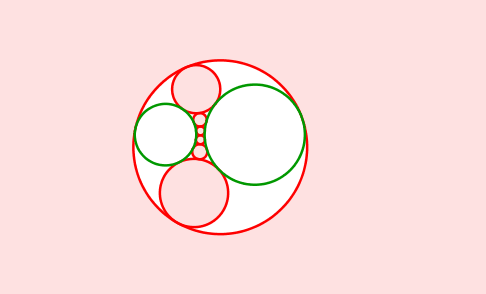
Abb. 14: Grüne Kreise nebeneinander

Die Mittelpunkte der roten Kreise bewegen sich auf einer Hyperbel. Diese hat die Mittelpunkte der grünen Kreise als Brennpunkte.

6.3 Kreis und Gerade. Parabolischer Fall

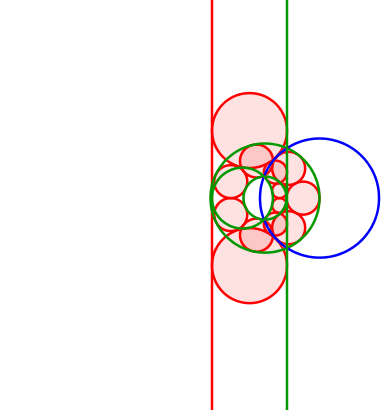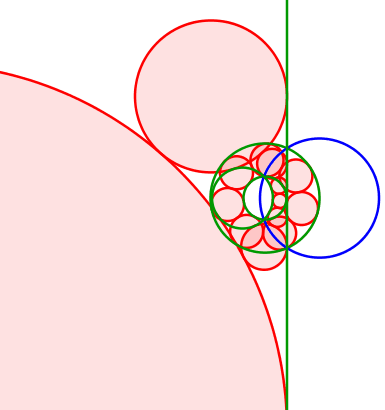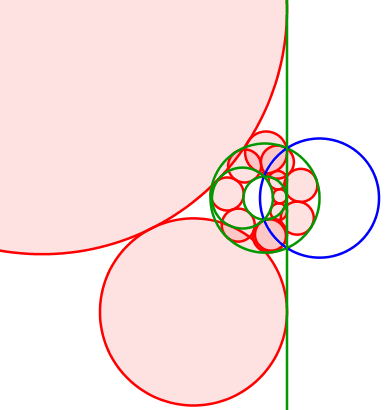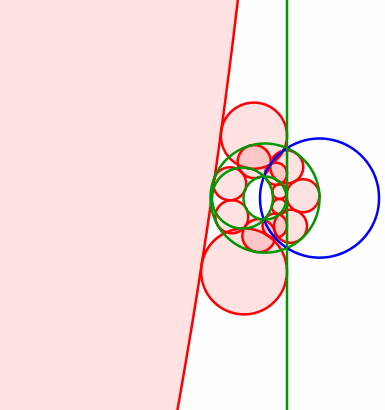
Abb. 15: Kreis und Gerade

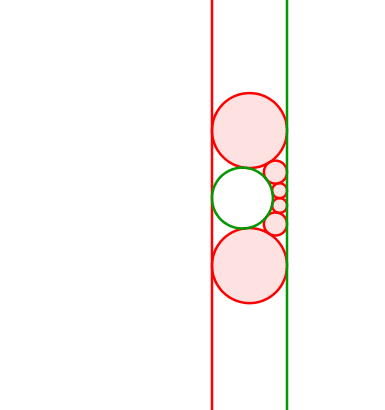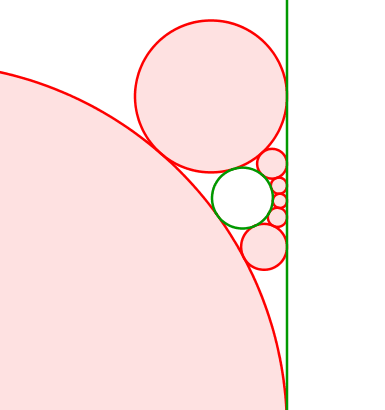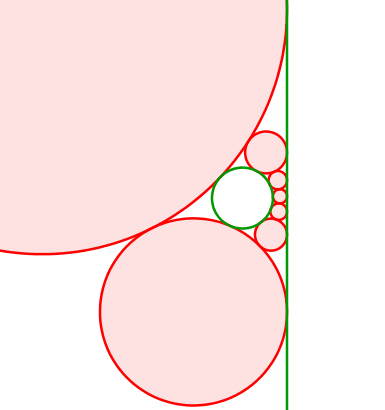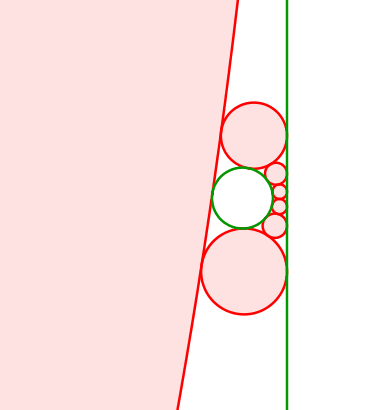
Abb. 16: Kreis und Gerade

Die Mittelpunkte der roten Kreise bewegen sich auf einer liegenden Parabel. Diese hat den Mittelpunkt des grünen Kreises als Brennpunkt. Die Leitlinie ist parallel zur grünen Gerade (rechts davon) und hat von dieser den Radius des grünen Kreises als Abstand.