Hans Walser, [20220830]
Stella vigintangula
1 Worum geht es?
Sternfigur mit 20 Spitzen auf der Basis des regelmäßigen Dodekaeders. Die Figur kann als Ikosaeder interpretiert werden.
2 Diagonalen im Dodekaeder
Wir arbeiten mit dem Kantenmodell des regelmäßigen Dodekaeders (Abb. 1).
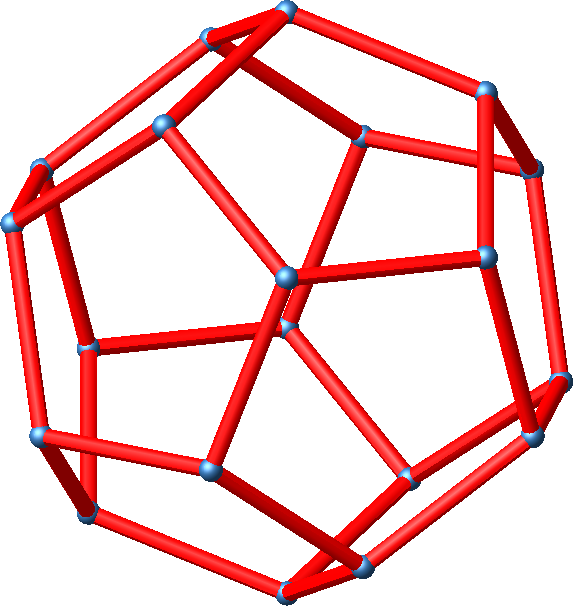
Abb. 1: Regelmäßiges Dodekaeder
In dieses Dodekaeder zeichnen wir sämtliche Diagonalen ein (Abb. 2).
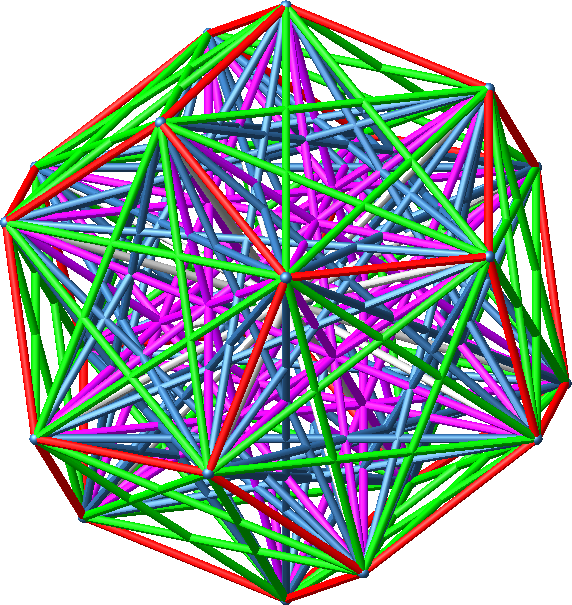
Abb. 2: Diagonalen
Die Diagonalen lassen sich wie folgt sortieren (Tab. 1). Dabei ist Φ der Goldene Schnitt:
![]()
|
Farbe |
Länge |
Länge approximativ |
Abstand der Endpunkte auf Kantengraf (Hamming-Länge) |
Anzahl |
Kommentar |
|
rot |
1 |
1 |
1 |
30 |
Dodekaederkanten |
|
grün |
Φ |
1.618033988 |
2 |
60 |
Seitenflächendiagonalen |
|
blau |
Φ√2 |
2.288245610 |
3 |
60 |
|
|
magenta |
Φ2 |
2.618033986 |
4 |
30 |
|
|
grau |
Φ√3 |
2.802517076 |
5 |
10 |
Mittelpunktsdiagonalen |
|
|
|
|
|
190 |
total = binomial(20, 2) |
Tab. 1: Anzahlen der Diagonalen
3 Diagonalenstern
Wir arbeiten im Folgenden ausschließlich mit den blauen Diagonalen (Abb. 3). Diese bilden einen Stern (Abb. 4).
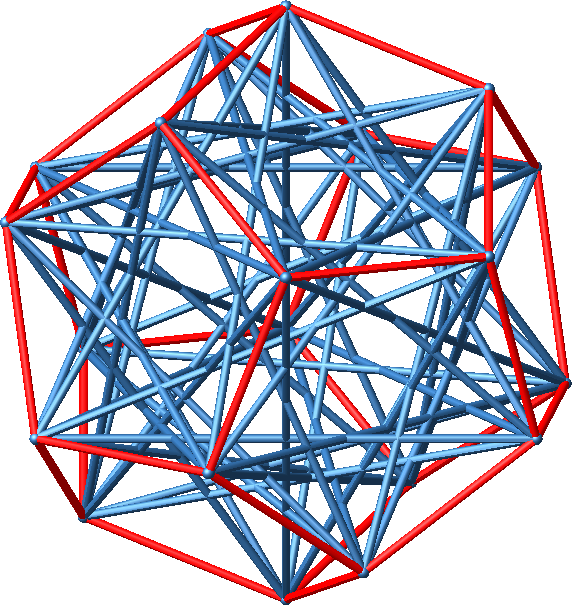
Abb. 3: Blaue Diagonalen

Abb. 4: Diagonalenstern
4 Gleichseitige Dreiecke
Im Diagonalenstern sehen wir gleichseitige Dreiecke (Abb. 5). Es gibt insgesamt 40 solche gleichseitige Dreiecke.

Abb. 5: Gleichseitiges Dreieck
Allerdings ist es so, dass in derselben Ebene jeweils zwei gleichseitige Dreiecke liegen (Abb. 6).

Abb. 6: Dreieckspaar in derselben Ebene
Das Dreieckspaar bildet einen unregelmäßigen Davidstern, wie man aus der Sicht von oben sieht (Abb. 7).

Abb. 7: Unregelmäßiger David-Stern
Die beiden Dreiecke sind um den Winkel δ verdreht mit:
Das ist kein „schöner“ Winkel, man beachte aber, dass die in der Formel erscheinenden natürlichen Zahlen 2, 3, 5, 8 aufeinanderfolgende Fibonacci-Zahlen sind.
Beim regelmäßigen David-Stern ist der Verdrehungswinkel 60°.
5 Tetraeder
Wir finden in der Figur auch Tetraeder (Abb. 8).

Abb. 8: Tetraeder
Das Dodekaeder enthält 10 solche Tetraeder.
Entsprechend zu den Dreieckspaaren in derselben Ebene gibt es Tetraederpaare mit einer Seite in derselben Ebene (Abb. 9). Sie haben eine Ecke gemeinsam.

Abb. 9: Tetraederpaar
6 Stella octangula
Wir finden auch Kepler-Sterne (stella octangula) (Abb. 10).

Abb. 10: Stella octangula
Es gibt entsprechend Paare von verdrehten Keplersternen (Abb. 11). Sie haben zwei diametrale Ecken gemeinsam.

Abb. 11: Paar von Kepler-Sternen
Das Dodekaeder enthält insgesamt fünf Kepler-Sterne (Abb. 12). Man kann sich überlegen, wie das mit der Paarbildung funktioniert.

Abb. 12: Fünf Kepler-Sterne
7 Stella vigintangula
Die fünf Keplersterne zusammen bilden die stella vigintangula, also einen Stern mit 20 Spitzen (Abb. 13 und 14).

Abb. 13: Stella vigintangula

Abb. 14: Stella vigintangula
8 Übersicht
|
|
|
Anzahl |
Kommentar |
|
Ecken |
e |
20 |
Ecken des Dodekaeders |
|
Kanten |
k |
60 |
Diagonalen der Hamming-Länge 3 |
|
Flächen |
f |
40 |
Gleichseitige Dreiecke |
|
David-Sterne |
|
20 |
Unregelmäßige David-Sterne |
|
Tetraeder |
|
10 |
|
|
Kepler-Sterne |
|
5 |
|
Tab. 2: Übersicht
Es ist e – k + f = 0.
Werden die Dreieckspaare zusammengefasst als Seitenfläche angesehen, haben wir eine Figur mit 20 Seitenflächen, also ein Ikosaeder (Coxeter et alii, 1938).
Weblinks
Hans Walser: Diagonalen platonischer Körper
http://www.walser-h-m.ch/hans/Miniaturen/D/Diag_platon_Koerper/Diag_platon_Koerper.html
Hans Walser: Ikosaeder-Stern
http://www.walser-h-m.ch/hans/Miniaturen/I/Ikosaeder-Stern/Ikosaeder-Stern.html
Literatur
Coxeter, H. S. M. / Du Val , P. / H.T. Flather, H. T. / Petrie, J. F. (1938): The Fifty-Nine Icosahedra. With 20 Plates and 9
Figures. New York: Springer 1938. ISBN 0-387-90770-X