Hans Walser, [20141129a], [20141201]
Sterbende Kaninchen
1 Beispiele
1.1 Sterben nach dem zweiten Wurf
Wir Šndern die Ÿbliche Kaninchen-Aufgabe von Fibonacci so ab, dass die Kaninchenpaare nach dem Wurf des zweiten Kaninchenpaares sterben.
Die Abbildungen 1 und 2 zeigen den Baum.
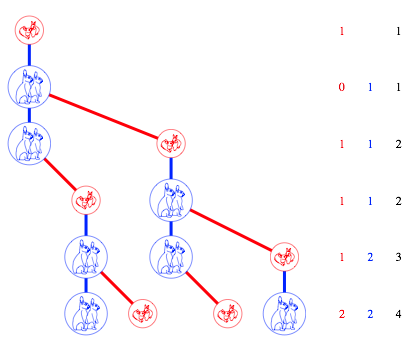
Abb. 1: Baum
Zu jeder Generation geben die roten Zahlen die Anzahl der jungen Paare, die blauen Zahlen die Anzahl der erwachsenen Paare und die schwarzen Zahlen die Totalzahl der Paare an.
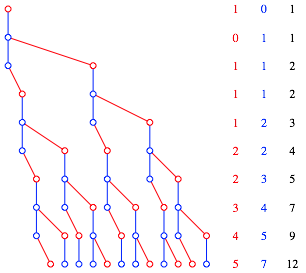
Abb. 2: Baum
FŸr alle drei Folgen gilt die Rekursion:
Die
Tabelle 1 gibt die Totalzahlen fŸr die ersten 20 Generationen. Es sind auch die
Wachstumsfaktoren 
angegeben.
|
n |
|
|
|
n |
|
|
|
1 |
1 |
1. |
|
11 |
16 |
1.312500000 |
|
2 |
1 |
2. |
|
12 |
21 |
1.333333333 |
|
3 |
2 |
1. |
|
13 |
28 |
1.321428571 |
|
4 |
2 |
1.500000000 |
|
14 |
37 |
1.324324324 |
|
5 |
3 |
1.333333333 |
|
15 |
49 |
1.326530612 |
|
6 |
4 |
1.250000000 |
|
16 |
65 |
1.323076923 |
|
7 |
5 |
1.400000000 |
|
17 |
86 |
1.325581395 |
|
8 |
7 |
1.285714286 |
|
18 |
114 |
1.324561404 |
|
9 |
9 |
1.333333333 |
|
19 |
151 |
1.324503311 |
|
10 |
12 |
1.333333333 |
|
20 |
200 |
1.325000000 |
Tab. 1: Anzahlen und Wachstumsfaktoren
Der Limes
genŸgt der kubischen Gleichung:
Diese hat die reelle Lšsung:
Wir haben nŠherungsweise ein exponentielles Wachstum.
Die Abbildung 3 zeigt die grafische Lšsung der kubischen Gleichung.
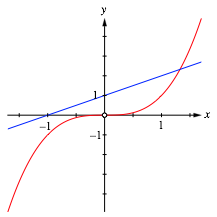
Abb. 3: Grafische Lšsung
1.2 Sterben nach dem dritten Wurf
Die Abbildung 4 zeigt den Baum fŸr die Situation, dass die Kaninchenpaare nach dem dritten Wurf sterben.
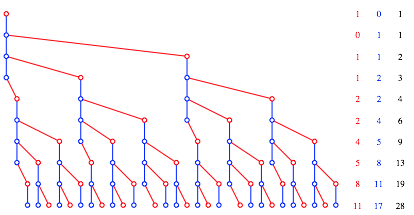
Abb. 4: Baum
Die drei Folgen sind nicht gleich, haben aber alle die gleiche Rekursion:
Die
Tabelle 2 gibt die Totalzahlen fŸr die ersten 20 Generationen. Es sind auch die
Wachstumsfaktoren 
angegeben.
|
n |
|
|
|
n |
|
|
|
1 |
1 |
1. |
|
11 |
41 |
1.463414634 |
|
2 |
1 |
2. |
|
12 |
60 |
1.466666667 |
|
3 |
2 |
1.500000000 |
|
13 |
88 |
1.465909091 |
|
4 |
3 |
1.333333333 |
|
14 |
129 |
1.465116279 |
|
5 |
4 |
1.500000000 |
|
15 |
189 |
1.465608466 |
|
6 |
6 |
1.500000000 |
|
16 |
277 |
1.465703971 |
|
7 |
9 |
1.444444444 |
|
17 |
406 |
1.465517241 |
|
8 |
13 |
1.461538462 |
|
18 |
595 |
1.465546218 |
|
9 |
19 |
1.473684211 |
|
19 |
872 |
1.465596330 |
|
10 |
28 |
1.464285714 |
|
20 |
1278 |
1.465571205 |
Tab. 2: Anzahlen und Wachstumsfaktoren
Der Limes
genŸgt der Gleichung vierten Grades:
Diese hat
neben der trivialen Lšsung 
die reelle
Lšsung:
Wir haben nŠherungsweise ein exponentielles Wachstum.
Die Abbildung 5 zeigt die grafische Lšsung der Gleichung vierten Grades.
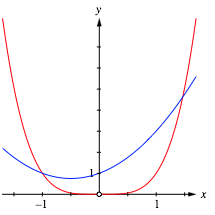
Abb. 5: Grafische Lšsung
1.3 Sterben nach dem vierten Wurf
Die Abbildung 6 zeigt den Baum fŸr die Situation, dass die Kaninchenpaare nach dem vierten Wurf sterben.
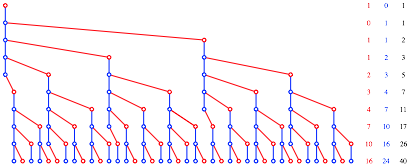
Abb. 6: Baum
Die drei Folgen sind nicht gleich, haben aber alle die gleiche Rekursion:
Die
Tabelle 3 gibt die Totalzahlen fŸr die ersten 20 Generationen. Es sind auch die
Wachstumsfaktoren 
angegeben.
|
n |
|
|
|
n |
|
|
|
1 |
1 |
1. |
|
11 |
61 |
1.540983607 |
|
2 |
1 |
2. |
|
12 |
94 |
1.531914894 |
|
3 |
2 |
1.500000000 |
|
13 |
144 |
1.534722222 |
|
4 |
3 |
1.666666667 |
|
14 |
221 |
1.533936652 |
|
5 |
5 |
1.400000000 |
|
15 |
339 |
1.533923304 |
|
6 |
7 |
1.571428571 |
|
16 |
520 |
1.534615385 |
|
7 |
11 |
1.545454545 |
|
17 |
798 |
1.533834586 |
|
8 |
17 |
1.529411765 |
|
18 |
1224 |
1.534313725 |
|
9 |
26 |
1.538461538 |
|
19 |
1878 |
1.534078807 |
|
10 |
40 |
1.525000000 |
|
20 |
2881 |
1.534189518 |
Tab. 3: Anzahlen und Wachstumsfaktoren
Der Limes
genŸgt der Gleichung fŸnften Grades:
Diese hat
im Intervall 
die Lšsung
. Wir haben nŠherungsweise ein exponentielles Wachstum.
Die Abbildung 7 zeigt die grafische Lšsung der Gleichung fŸnften Grades.
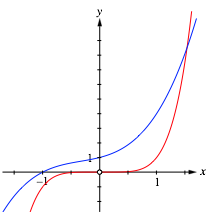
Abb. 7: Grafische Lšsung
2 Allgemein
Beim Absterben nach dem k-ten Wurf ergibt sich die Rekursion:
Die 
Startwerte
sind die Fibonacci-Zahlen. Der Limes
genŸgt der Gleichung vom Grad k + 1:
Die
Tabelle 4 zeigt die Grenzwerte 
in
AbhŠngigkeit von k.
|
k |
|
|
|
k |
|
|
1 |
1. |
|
|
26 |
1.618032341 |
|
2 |
1.324717957 |
|
|
27 |
1.618032970 |
|
3 |
1.465571232 |
|
|
28 |
1.618033359 |
|
4 |
1.534157745 |
|
|
29 |
1.618033600 |
|
5 |
1.570147312 |
|
|
30 |
1.618033748 |
|
6 |
1.590005374 |
|
|
31 |
1.618033840 |
|
7 |
1.601347334 |
|
|
32 |
1.618033897 |
|
8 |
1.607982728 |
|
|
33 |
1.618033932 |
|
9 |
1.611930397 |
|
|
34 |
1.618033954 |
|
10 |
1.614306823 |
|
|
35 |
1.618033967 |
|
11 |
1.615749203 |
|
|
36 |
1.618033975 |
|
12 |
1.616629684 |
|
|
37 |
1.618033980 |
|
13 |
1.617169296 |
|
|
38 |
1.618033984 |
|
14 |
1.617500905 |
|
|
39 |
1.618033986 |
|
15 |
1.617705070 |
|
|
40 |
1.618033987 |
|
16 |
1.617830929 |
|
|
41 |
1.618033988 |
|
17 |
1.617908582 |
|
|
42 |
1.618033988 |
|
18 |
1.617956520 |
|
|
43 |
1.618033988 |
|
19 |
1.617986125 |
|
|
44 |
1.618033988 |
|
20 |
1.618004414 |
|
|
45 |
1.618033989 |
|
21 |
1.618015713 |
|
|
46 |
1.618033989 |
|
22 |
1.618022695 |
|
|
47 |
1.618033989 |
|
23 |
1.618027009 |
|
|
48 |
1.618033989 |
|
24 |
1.618029675 |
|
|
49 |
1.618033989 |
|
25 |
1.618031323 |
|
|
50 |
1.618033989 |
Tab. 4: Wachstumsfaktoren
Die Wachstumsfaktoren streben gegen den Goldenen Schnitt.
Beweisskizze:
Die Gleichung
kann umgeformt werden zu
FŸr 
verschwindet bei 
der
Stšrterm 
. †brig bleibt die quadratische Gleichung 
mit der
Lšsung des Goldenen Schnittes 
.