Hans Walser, [20160409]

Stereografische Projektion

Idee und Anregung: R. S., C.

1     Problemstellung

Gegeben sind die vier Funktionen:

 

                                       (1)

 

Fźr eine reelle Zahl z werden die vier Punkte

 

                     (2)

 

gebildet. Welche Eigenschaften haben die Vierecke ABCD?

Die Abbildung 1 zeigt die Situation fźr ganze Zahlen .

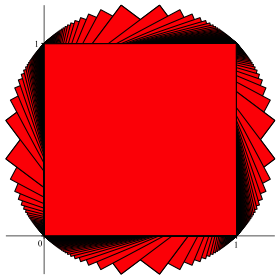
Abb. 1: Ganzzahlige Parameter

2     Bearbeitung

Wir transformieren die Situation. Wir schieben den Punkt  in den Ursprung und skalieren mit dem Faktor . Damit wird:

 

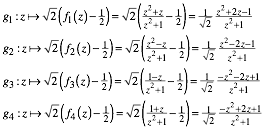                                                 (3)

 

Es ist:

 

                                                                                                               (4)

 

Aus der Symmetrie der Abbildungsgleichungen (3) und (4) folgt sofort, dass die Vierecke Quadrate mit Zentrum im Ursprung sind.

Wegen

 

                                                       (5)

 

haben diese Quadrate den Einheitskreis als gemeinsamen Umkreis.

Die Abbildung 2 zeigt die neue Situation im Koordinatensystem.

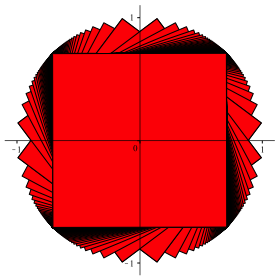
Abb. 2: Zentrierte Situation

Auffallend sind fźr  die HŠufungspunkte bei den Quadratecken. Dazu folgende ErklŠrung.

3     Stereografische Projektion

Wegen der vierteiligen Drehsymmetrie der Quadrate kšnnen wir uns auf eine Quadratecke beschrŠnken. Die Abbildung 3 zeigt die Ecken A fźr .

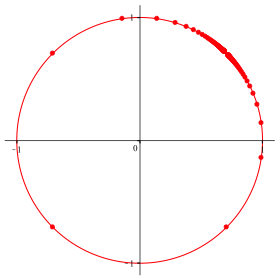
Abb. 3: Verteilung auf dem Einheitskreis

3.1    Vermutung

Die Verteilung der Punkte A auf dem Einheitskreis lŠsst eine stereografische Projektion vermuten.

Die stereografische Projektion (in der Ebene) ist eine Zentralprojektion des Kreises von einem Kreispunkt (blau in Abb. 4) aus auf die Tangente im gegenźberliegenden Kreispunkt.

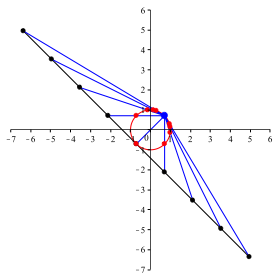
Abb. 4: Stereografische Projektion

Wir vermuten in unserem Beispiel, dass eine Šquidistante Punktefolge (schwarz) mit der €quidistanz 2 auf der Tangente auf den Kreis (rote Punkte) rźckprojiziert wird. Das erklŠrt auch, warum das (blaue) Projektionszentrum zum HŠufungspunkt der roten Punkte wird.

3.2    Beweis

Wegen (5) ist folgende Substitution zulŠssig:

 

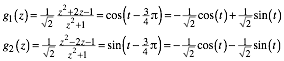                                           (6)

 

Daraus ergibt sich:

 

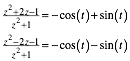                                                                                               (7)

 

Addition und Subtraktion der beiden Gleichungen (7) liefert:

 

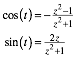                                                                                                                 (8)

 

Daraus folgt:

 

                                                                                                                   (9)

 

Vergleich mit dem Additionstheorem des Tangens

 

                                                                                     (10)

 

liefert:

 

                                                                                                                     (11)

 

Die Abbildung 5 zeigt die stereografische Projektion in der źblichen Darstellung.

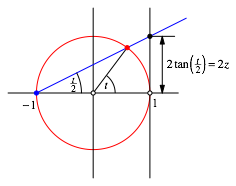
Abb. 5: Stereografische Projektion

Wir sehen, dass sich fźr  eine Šquidistante Punktfolge mit der €quidistanz 2 ergibt.