Hans Walser, [20201217]
Stereografische Projektion
1 Worum geht es?
Darstellung der platonischen Krper in stereografischer Projektion. Schlegel Diagramm. Fcher-Konstruktionen.
2 Vorgehen
Zum gegebenen platonischen Krper zeichnen wir die Umkugel. Senkrecht ber der Mitte einer Seitenflche whlen wir das Projektionszentrum (blau eingezeichnet). Der platonische Krper wird so in den Raum gestellt, dass dieses Projektionszentrum oben ist (Nordpol). Als Projektionsebene whlen wir die quatorebene oder eine dazu parallele Ebene, zum Beispiel die Bodenebene. Die Wahl der Parallelebene hat keinen Einfluss auf das projizierte Bild.
Der platonische Krper wird als Kantenmodell gezeichnet, wobei die Kanten als Zylinder gezeichnet werden. Man kann also auch von einem Drahtmodell sprechen. Die Ecken werden durch eingepasste Kugeln mit dem Zylinderdurchmesser abgerundet.
Diese Art der Darstellung hat zur Folge, dass die Kanten in der Nhe des Projektionszentrums (also die oberen Kanten) sehr dick gezeichnet werden, die entfernteren Kanten dnner. In die Tiefe laufende Kanten werden zunehmend dnner (perspektivische Verkrzung).
Das Schlegel-Diagramm wird mit derselben Geometrie, aber ohne perspektivische Verkrzung gezeichnet. Die Schlegel-Diagramme der stereografisch projizierten platonischen Krper knnen mit interessanten Fcher-Konstruktionen in der Ebene gezeichnet werden.
3 Die platonischen Krper
3.1 Tetraeder
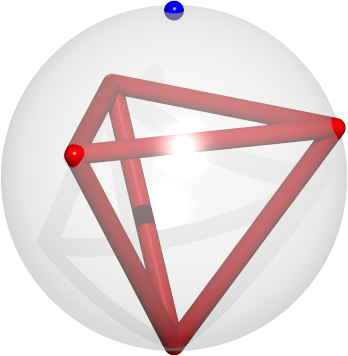
Abb. 1: Tetraeder mit Umkugel und Projektionszentrum

Abb. 2: Stereografische Projektion
Die Konstruktion des Schlegel-Diagramms ergibt sich durch Winkelhalbierende (Abb. 3).
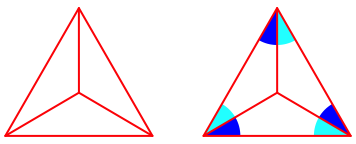
Abb. 3: Schlegel-Diagramm
3.2 Hexaeder (Wrfel)

Abb. 4: Wrfel mit Umkugel und Projektionszentrum

Abb. 5: Stereografische Projektion
Die Abbildung 6 zeigt das Schlegel-Diagramm zusammen mit seiner Konstruktion. Das gelbe Dreieck ist gleichseitig.
Als Projektionsebene dient zunchst die Ebene des Deckquadrates des Wrfels. Dann wird die Figur dem Betrachter vorgestellt.
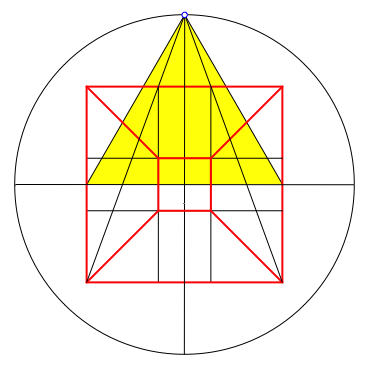
Abb. 6: Schlegel-Diagramm
Einfacher, aber nicht so leicht verstndlich (Nachweis durch Rechnung), ist die Fchermethode (Abb. 7). Die blauen und hellblauen Fcherwinkel messen je 15¡.

Abb. 7: Fcher
3.3 Oktaeder
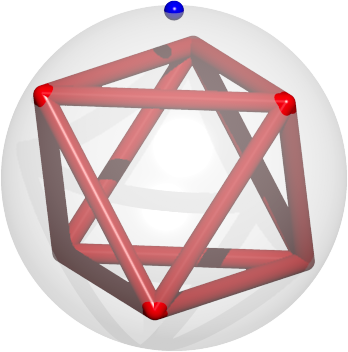
Abb. 8: Oktaeder mit Umkugel und Projektionszentrum

Abb. 9: Stereografische Projektion
Die Abbildung 10 zeigt die Konstruktion des Schlegel-Diagramms auf der Basis eines geviertelten DIN-Rechteckes (gelb). Der orange Rhombus gibt eine Seitenansicht des Oktaeders. Als Projektionsebene dient die Ebene des Deckdreieckes des Oktaeders. Dann wird die Figur dem Betrachter vorgestellt.
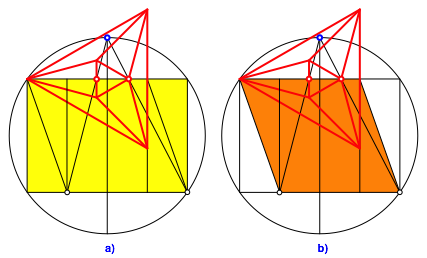
Abb. 10: Konstruktion des Schlegel-Diagramms
Viel einfacher, aber nicht so leicht verstndlich (Herleitung folgt), ist die Fchermethode (Abb. 11). Die blauen und hellblauen Fcherwinkel messen wie beim Wrfel je 15¡.
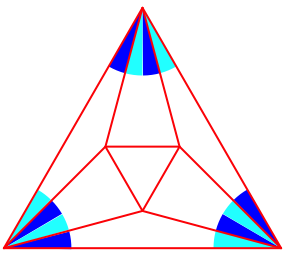
Abb. 11: Fcher
Fr die
Herleitung der Fchermethode arbeiten wir mit den Daten der Abbildung 12. Sie
basiert auf der Abbildung 10a. Wir berechnen den Zwischenwinkel ![]() der beiden
Vektoren
der beiden
Vektoren ![]() und
und ![]() .
.
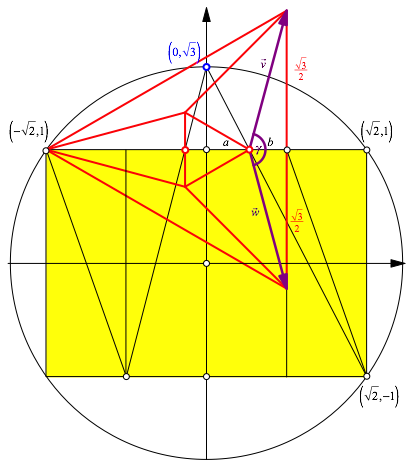
Abb. 12: Beweisfigur
Fr die eingezeichnete Strecke a gilt:
![]() (1)
(1)
Daraus erhalten wir fr die Strecke b:
![]() (2)
(2)
Fr den
Vektor ![]() ergibt
sich:
ergibt
sich:
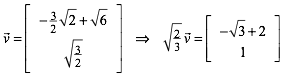 (3)
(3)
Analog:
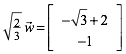 (4)
(4)
Daraus erhalten wir:
![]() (5)
(5)
Damit ist die Stimmigkeit der Fcher-Konstruktion der Abbildung 11 gezeigt.
3.4 Dodekaeder
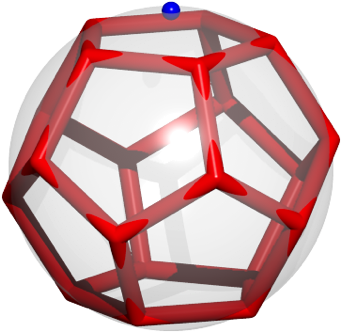
Abb. 13: Dodekaeder

Abb. 14: Dodekaeder in stereografischer Projektion
Die Abbildung 15 zeigt das Schlegel-Diagramm, gezeichnet mit den klassischen Methoden der darstellenden Geometrie.

Abb. 15: Schlegel-Diagramm
Smtliche Eckpunkte des Schlegel-Diagramms lassen sich durch die Fcher der Abbildung 16 konstruieren. Der Fcherwinkel misst 6¡. Verifikation mit DGS.
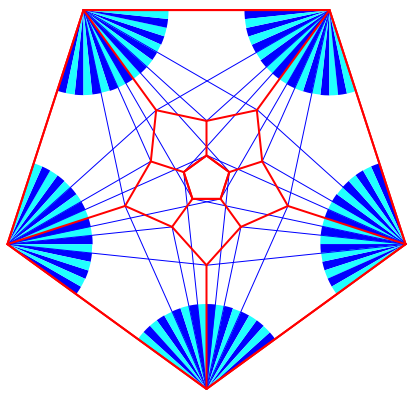
Abb. 16: Fcher
3.5 Ikosaeder
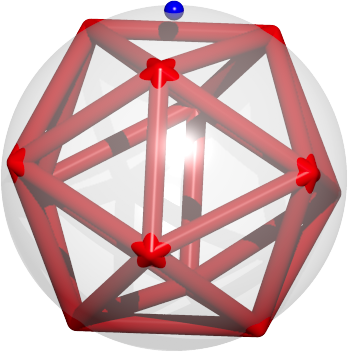
Abb. 17: Ikosaeder

Abb. 18: Ikosaeder in stereografischer Projektion
In der Abbildung 18 sind einige Kanten durch die dicken Kanten im Vordergrund verdeckt.
Die Abbildung 19 zeigt eine Version mit dnneren Kanten.
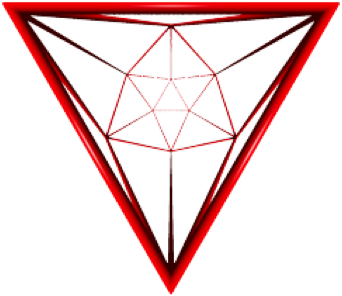
Abb. 19: Dnne Kanten
Die Abbildung 20 zeigt das Schlegel-Diagramm, lege artis gezeichnet.

Abb. 20: Schlegel-Diagramm
Der Fcher-Trick funktioniert auch hier (Abb. 21). Der Fcherwinkel ist wie beim Dodekaeder 6¡. Verifikation mit DGS.
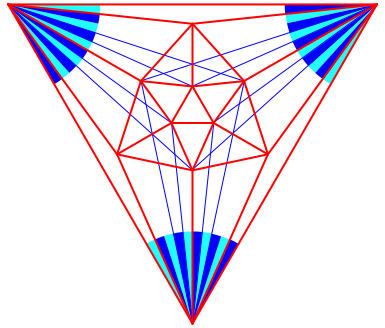
Abb. 21: Fcher
4
Eine Invariante
Es besteht ein Zusammenhang zwischen dem Fcherwinkel und der Kantenzahl (Tab. 1).
|
Polyeder |
Kantenzahl |
Fcherwinkel |
Produkt |
|
Tetraeder |
6 |
30¡ |
180¡ |
|
Wrfel/Oktaeder |
12 |
15¡ |
180¡ |
|
Dodekaeder/Ikosaeder |
30 |
6¡ |
180¡ |
Tab.
1: Kantenzahl und Fcherwinkel
Websites
Hans
Walser: Ikosaeder
https://www.walser-h-m.ch/hans/Miniaturen/I/Ikosaeder/Ikosaeder.htm
Hans
Walser: Kuboktaeder
http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder/Kuboktaeder.htm
Hans
Walser: Semiregulres Ikosaeder
http://www.walser-h-m.ch/hans/Miniaturen/S/Semireg_Ikosaeder/Semireg_Ikosaeder.htm
Hans
Walser: Stereografische Projektion
http://www.walser-h-m.ch/hans/Miniaturen/S/Stereo_Proj_4/Stereo_Proj_4.htm