Hans Walser, [20160912]

Anregung: Manfred Schmelzer, Regensburg

Stern im Viereck

1 Worum geht es

Es wird eine Sternfigur im Viereck (Abb. 1) besprochen.

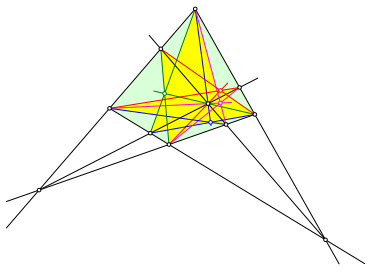
Abb. 1: Stern im Viereck

2 Schnittpunkt

Im Viereck finden wir einen Schnittpunkt von drei Geraden wie folgt: Wir beginnen mit einem beliebigen Viereck und wählen darin einen Punkt (Abb. 2).

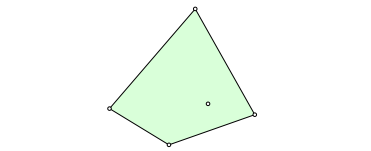
Abb. 2: Viereck mit Punkt

Wir ergänzen die Figur gemäß Abbildung 3.

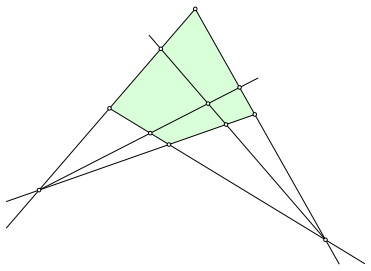
Abb. 3: Ergänzung der Figur

In dieser Figur finden wir drei kopunktale Geraden (rot in Abb. 4).

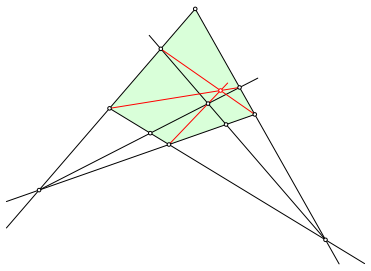
Abb. 4: Schnittpunkt dreier Geraden

In der Abbildung 1 sind noch drei weitere Beispiele von je drei kopunktalen Geraden (dunkelgrün, blau, magenta) eingezeichnet.

3 Beweis

Die in der Figur der Abbildung 4 vorkommenden Begriffe Gerade und Schnittpunkt sind projektiv invariant.

Für den Beweis der Schnittpunkteigenschaft können wir daher das grüne Viereck mit einer projektiven Abbildung auf ein Standardviereck, zum Beispiel das Einheitsquadrat in einem kartesischen Koordinatensystem, abbilden (Abb. 5). Die beiden in der Abbildung 4 eingetragenen Schnittpunkte je zweier gegenüberliegender Viereckseiten gehen dabei ins Unendliche.

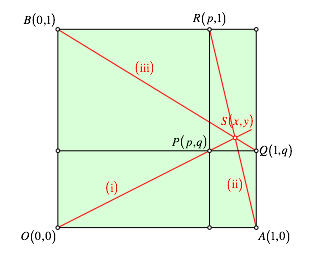
Abb. 5: Situation im Einheitsquadrat

Der Rest ist Rechnung. Für die drei roten Geraden erhalten wir die Gleichungen:

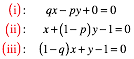(1)

Die Determinante der Koeffizientenmatrix verschwindet:

(2)

Damit sind die drei Geraden kopunktal.

Der Schnittpunkt S hat in Abhängigkeit der Koordinaten von P die Koordinaten:

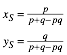(3)

4 Weitere Schnittpunkte

Aus strukturellen Symmetriegründen gibt es insgesamt vier Schnittpunkte (Abb. 6). Wir können dazu einen Stern mit acht Spitzen einzeichnen.

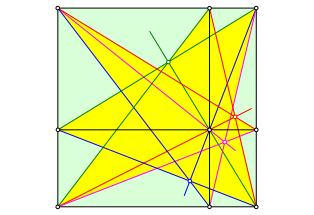
Abb. 6: Stern im Quadrat

5 Abbildung

Wir können (3) als Abbildungsgleichungen interpretieren. Die Abbildung 7 zeigt diese Abbildung im Zehntelraster.

Abb. 7: Abbildung von P nach S

Die Abbildung 8 zeigt entsprechend alle Lösungen.

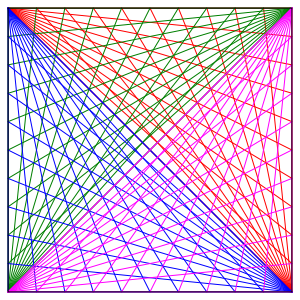
Abb. 8: Die vier Schnittpunkte

6 Sonderfälle

6.1 Binomische Formel und Pythagoras

Die Abbildung 9a zeigt eine altgediente Illustrations- und Beweisfigur für die binomische Formel und den Satz des Pythagoras.

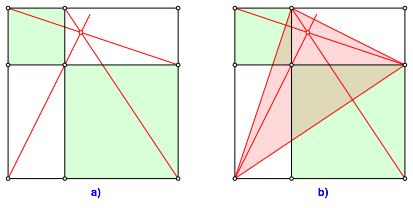
Abb. 9: Binomische Formel und Pythagoras

In diesem Sonderfall können wir ein Dreieck einzeichnen (rot in Abbildung 9b), dessen Höhen unsere roten Linien sind. Wir können diesen Sonderfall also viel einfacher beweisen.

6.2 Figur von Knauth

Die Abbildung 10 zeigt als extremen Sonderfall die Figur von Knauth (Hoehn und Walser, 2003). Die Schnittpunkteigenschaft ist aus Symmetriegründen trivial.

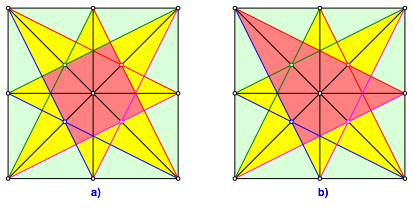
Abb. 10: Figur von Knauth

Der Flächeninhalt des roten Quadrates in der Abbildung 10a ist ein Fünftel des Flächeninhaltes des grünen Quadrates. Das rote Dreieck in der Abbildung 10b ist ein pythagoreisches Dreieck mit dem Seitenverhältnis 3:4:5. Es hat viele weitere solche pythagoreische Dreiecke in der Figur.

7 Dualität

Die Abbildung 11 zeigt ein nicht konvexes Viereck. Tatsächlich sind gegenüber der Abbildung 4 eine Ecke und der rote Schnittpunkt vertauscht worden. Daher die Sprechweise „Dualität“.

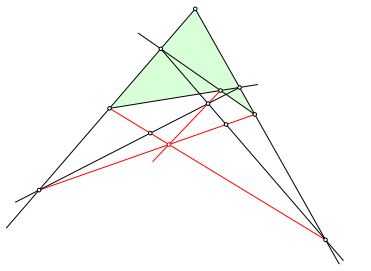
Abb. 11: Nicht konvexes Viereck

Literatur

Hoehn, Alfred und Walser, Hans (2003): Gittergeometrie und pythagoreische Dreiecke. Praxis der Mathematik (5/45), 215-217.