Hans Walser, [20150625]
Sterne
1 Worum geht es?
Es werden Verallgemeinerungen des Fibonacci-Sterns (Walser 2012, S. 31 und Walser 2013, S. 108) und des Goldenen Sterns (Walser 2013, S. 109) vorgestellt.
2 Verallgemeinerung des Fibonacci-Sterns
2.1 Beispiel
Wir illustrieren das Verfahren an einem Beispiel mit einem Stern mit k = 8 Spitzen.
Wir
beginnen gem§ Abbildung 1a mit einem gleichschenkligen Dreieck mit dem Spitzenwinkel
![]() . Dieses Dreieck hat die Basiswinkel 67.5¡.
. Dieses Dreieck hat die Basiswinkel 67.5¡.
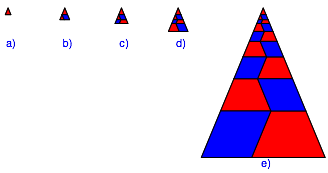
Abb. 1: Vorgehen fr k = 8
Unter dieses Dreieck passen wir rechts einen Rhombus mit dem spitzen Winkel 67.5¡ ein und daneben ein gleichschenkliges Dreieck gem§ Abbildung 1b. Dieses Dreieck ist hnlich zum Startdreieck.
Dann passen wir links unter das neue gleichschenklige Dreieck einen Rhombus mit dem spitzen Winkel 67.5¡ ein und rechts daneben ein gleichschenkliges Trapez (Abb. 1c). Dieses gleichschenklige Trapez hat Basiswinkel 67.5¡.
Weiter passen wir rechts unter das Trapez einen Rhombus ein und ergnzen links mit einem gleichschenkligen Trapez (Abb. 1d).
So fahren wir weiter und passen abwechslungsweise links und rechts Rhomben ein und ergnzen mit gleichschenkligen Trapezen (Abb. 1e). Es entsteht ein gro§es gleichschenkliges Dreieck mit dem Winkel 45¡ an der Spitze. Die Trapeze haben zwar alle die gleichen Winkel, sind aber nicht hnlich. Die Seitenverhltnisse differieren geringfgig.
Nun entfernen wir die Rhomben (Abb. 2a) und klappen die Trapeze (und die Dreiecke ganz oben) an den gelenkig gedachten gemeinsamen Punkten zusammen (Abb. 2b).
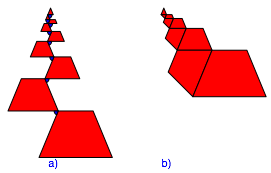
Abb. 2: Entfernen der Rhomben. Zusammenklappen
Mit k = 8 Kopien dieser Figur knnen wir nun einen Stern bauen (Abb. 3). Im Zentrum des Sterns erkennen wir ein regelm§iges Achteck.
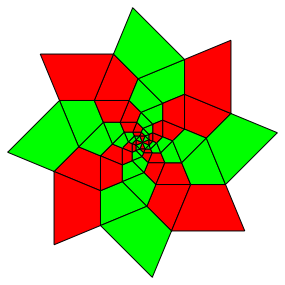
Abb. 3: Stern
Die Abbildung 4 zeigt den Stern in monochromer Ausfhrung.
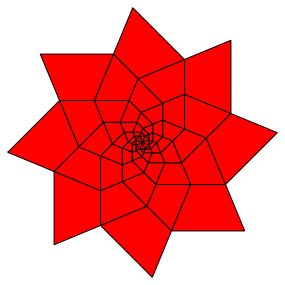
Abb. 4: Stern mit acht Spitzen
2.2 Zahlentheoretischer Hintergrund
Wir
definieren eine Zahlenfolge ![]() rekursiv
wie folgt.
rekursiv
wie folgt.
Startwerte:
![]()
Rekursion:
![]()
Das ist eine verallgemeinerte Fibonacci-Rekursion.
In unserem Beispiel mit k = 8 hei§t das:
![]()
Die Tabelle 1 gibt die ersten Werte.
|
n |
|
|
|
|
0 |
0 |
0 |
– |
|
1 |
1 |
1 |
0.7653668650 |
|
2 |
|
0.7653668650 |
2.071929830 |
|
3 |
|
1.585786438 |
1.248008693 |
|
4 |
|
1.979075260 |
1.566643336 |
|
5 |
|
3.100505066 |
1.403674242 |
|
6 |
|
4.352099098 |
1.477782876 |
|
7 |
|
6.43145752 |
1.442056260 |
|
8 |
|
9.274523581 |
1.458821090 |
|
9 |
|
13.5298706 |
1.450851875 |
|
10 |
|
19.62983813 |
1.454617140 |
Tab. 1: Zahlenfolge
Diese
Zahlen knnen im Dreieck der Abbildung 1 als Streckenlngen visuell dargestellt
werden gem§ Abbildung 5. Wer Lust hat, kann sich berlegen, wo die Null von ![]() steckt und
was es mit dem grnen Dreieck an der Spitze auf sich hat (Tipp: Folge ins
Negative fortsetzen).
steckt und
was es mit dem grnen Dreieck an der Spitze auf sich hat (Tipp: Folge ins
Negative fortsetzen).
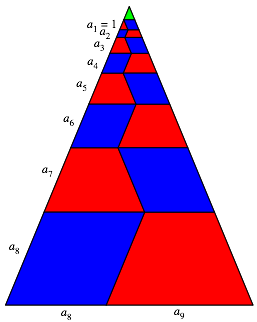
Abb. 5: Visualisierung
Die Abbildung 6 gibt exemplarisch eine Erklrung fr diesen Sachverhalt. Die Rekursion steckt in den Trapezen. Wir mssen in den Trapezen noch ein Parallelogramm einbauen, um die Rekursion sichtbar zu machen.
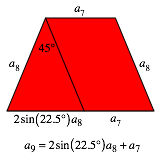
Abb. 6: Rekursion
Bemerkung:
Bei der Quotientenfolge ![]() vermuten
wir einen Limes. Dieser ist die positive Lsung der quadratischen Gleichung:
vermuten
wir einen Limes. Dieser ist die positive Lsung der quadratischen Gleichung:
![]()
Die Lsungen sind:
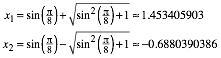
Herleitung gem§ allgemeinen Techniken bei der verallgemeinerten Fibonacci-Folge (Walser 2013, S. 113f).
2.3 Der Sonderfall
Fr k = 6 erhalten wir wegen ![]() die
Fibonacci-Rekursion und entsprechend die Fibonacci-Folge. Zur Visualisierung
dazu siehe (Plaza and Walser 2013).
die
Fibonacci-Rekursion und entsprechend die Fibonacci-Folge. Zur Visualisierung
dazu siehe (Plaza and Walser 2013).
2.4 Bildergalerie
Einige Beispiele.

Abb. 7: Drei Spitzen

Abb. 8: Vier Spitzen

Abb. 9: Fnf Spitzen
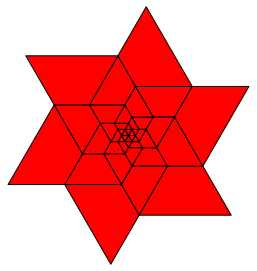
Abb. 10: Sechs Spitzen, Fibonacci-Stern

Abb. 11: Zehn Spitzen
Bei den bisherigen Beispielen war im Zentrum ein regelm§iges k-Eck zu erkennen. Das ndert sich bei den folgenden berlegungen.
3 Verallgemeinerung des Goldenen Sterns
3.1 Beispiel
Wiederum exemplarisch das Vorgehen fr einen Stern mit k = 8 Spitzen.
Die Schlsselzahl ist die positive Lsung der quadratischen Gleichung:
![]()
Also:
![]()
Wir
zeichnen nun ein gleichschenkliges Mustertrapez mit der Deckseite 1, der Schenkellnge
![]() und dem
Basiswinkel 67.5¡ (Abb. 12).
und dem
Basiswinkel 67.5¡ (Abb. 12).
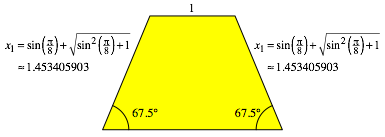
Abb. 12: Mustertrapez
Nun formen wir aus acht Trapezen einen Ring gem§ Abbildung 13a.
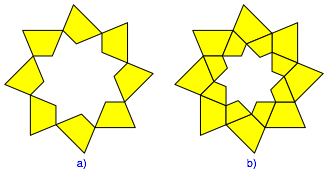
Abb. 13: Ring und Doppelring
Zu diesem
Ring erstellen wir eine spiegelbildliche Kopie, drehen sie um 22.5¡ und reduzieren
sie mit dem Kehrwert von ![]() . Dann passt die Kopie genau in den Ring der Abbildung
13a. Wir erhalten den Doppelring der Abbildung 13b.
. Dann passt die Kopie genau in den Ring der Abbildung
13a. Wir erhalten den Doppelring der Abbildung 13b.
Diesen
Doppelring knnen wir nun kopieren und mit Faktoren ![]() , strecken und einpassen. So entsteht ein Stern (Abb.
14).
, strecken und einpassen. So entsteht ein Stern (Abb.
14).
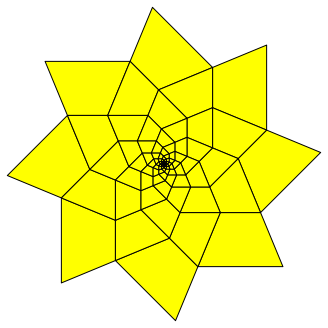
Abb. 14: Stern mit acht Spitzen
Im Unterschied zum Stern der Abbildung 4 erkennen wir im Zentrum kein regelm§iges Achteck. Vielmehr haben wir im Zentrum einen Hufungspunkt. Die Trapeze sind alle zueinander hnlich. Wir haben das Verhalten einer geometrischen Folge.
Der Stern ist eine Verallgemeinerung des Goldenen Sterns.
Wir erkennen im Stern eckige logarithmische Spiralen (Abb. 15).

Abb. 15: Eckige logarithmische Spiralen
3.2 Hintergrund
Die Trapeze in der Abbildung 4 haben zwar gleiche Winkel, nicht aber gleiche Seitenverhltnisse. Allerdings haben die Seitenverhltnisse einen Grenzwert. ãJanz weit au§enÒ nhern sich die Trapeze formm§ig einem Grenztrapez an. Fr die Verallgemeinerung des Goldenen Sterns beginnen wir gleich mit diesem Grenztrapez und ergnzen zum Stern.
3.3 Beispiele
Fr die Beispiele mit verschiedenen Spitzenzahlen k verschaffen wir und zunchst einen berblick ber die Grenzwerte der Seitenverhltnisse (Tab. 2).
|
k |
Grenzwert |
Grenzwert |
Kehrwert |
|
1 |
1 |
1 |
1 |
|
2 |
|
2.414213562 |
0.4142135624 |
|
3 |
|
2.188901060 |
0.4568502516 |
|
4 |
|
1.931851653 |
0.5176380901 |
|
5 |
|
1.747738485 |
0.5721679808 |
|
6 |
|
1.618033988 |
0.6180339890 |
|
7 |
|
1.523954883 |
0.6561874050 |
|
8 |
|
1.453405903 |
0.6880390385 |
|
9 |
|
1.398891837 |
0.7148515515 |
|
10 |
|
1.355674294 |
0.7376403052 |
Tab. 2: Grenzwerte
Die Zahlen k = 1 und k = 2 sind fr unseren geometrischen Kontext irrelevant.
Fr k = 6 erhalten wir den Goldenen Schnitt. Das ist insofern bemerkenswert, als wir blicherweise den Goldenen Schnitt im Zusammenhang mit der Zahl 5 antreffen.
Und nun einige Beispiele.
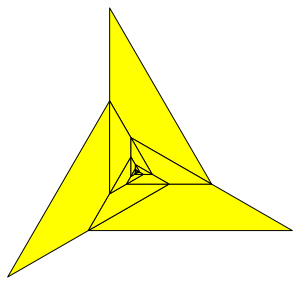
Abb. 16: Drei Spitzen

Abb. 17: Vier Spitzen
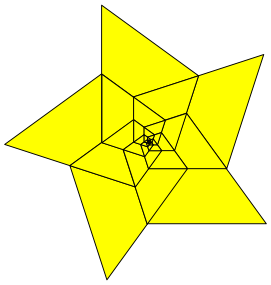
Abb. 18: Fnf Spitzen
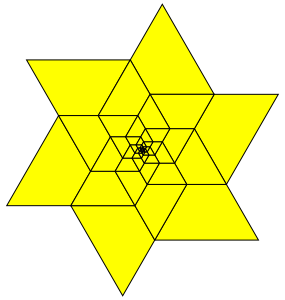
Abb. 19: Sechs Spitzen. Goldener Stern

Abb. 20: Zehn Spitzen
Literatur
Plaza, Angel and Walser, Hans (2013): Proof Without Words: Fibonacci Triangles and Trapezoids. Mathematics Magazine. 86 (2013) p. 55.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.