Hans Walser, [20130604b]
Anregung: H. M.-S., V.
Sternfigur
1 Dreieck mit Hhen
Wir beginnen mit einem beliebigen Dreieck und zeichnen die Hhen ein (Abb. 1).
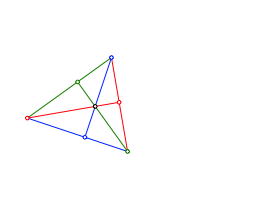
Abb. 1: Dreieck mit Hhen
2 Rechtwinklige Dreiecke ansetzen
Die Fu§punkte der Hhen unterteilen die Dreiecksseiten in je zwei Abschnitte. Diese verwenden wir als Katheten fr rechtwinklige Dreiecke, welche wir den Abschnitten gem§ Abbildung 2 ansetzen. Rechtwinklige Dreiecke gleicher Farbe sind also kongruent.

Abb. 2: Ansetzen von rechtwinkligen Dreiecken
3 Schnittpunkte
Nun verlngern wir die Hypotenusen dieser Dreiecke und die Hhen des Dreieckes. Je zwei Hypotenusen und eine Hhe schneiden sich in einem Punkt (Abb. 3). Numerisch verifiziert, Beweis steht noch aus.
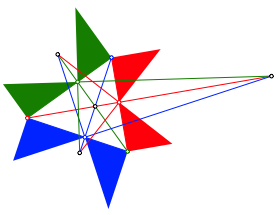
Abb. 3: Sternfigur
4 Variante
Wir zeichnen in einem beliebigen Dreieck zwei Hhen und eine Mittelsenkrechte gem§ Abbildung 4. Zustzlich setzen wir zwei rechtwinklig gleichschenklige Dreiecke an.
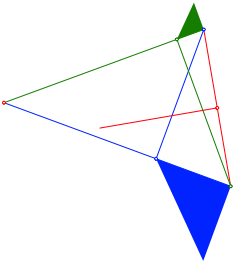
Abb. 4: Rechtwinklige gleichschenklige Dreiecke ansetzen
Die verlngerten Hypotenusen und die Mittelsenkrechte schneiden sich in einem Punkt (Abb. 5).
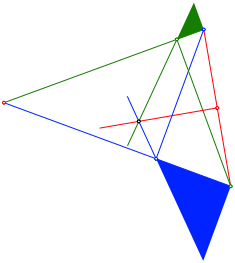
Abb. 5: Schnittpunkt
Mehr noch: Wir knnen ein weiteres rechtwinklig gleichschenkliges Dreieck einpassen (Abb. 6).
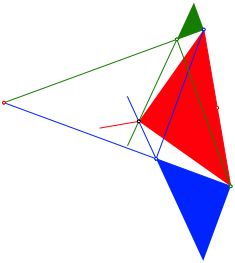
Abb. 6: Ein drittes rechtwinklig gleichschenkliges Dreieck
Natrlich lsst sich das jetzt fr die anderen Seiten wiederholen, die Gesamtfigur wird aber unbersichtlich.
5 Gleichseitiges Dreieck
Am gleichseitigen Dreieck sind die anzusetzenden rechtwinkligen Dreiecke aus Symmetriegrnden gleichschenklig (Abb. 7).

Abb. 7: Gleichseitiges Dreieck
Die Schnittpunkteigenschaft ist aus Symmetriegrnden trivial (Abb. 8). Die Schnittpunkte liegen auf dem Rand der konvexen Hlle der Figur der Abbildung 7.
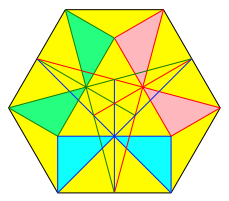
Abb. 8: Schnittpunkte auf Umriss
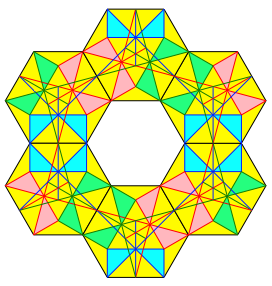
Abb. 9: Ring
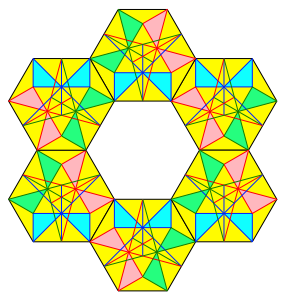
Abb. 10: Ring