Hans Walser, [20141017]
Sternfigur
1 Worum geht es?
Auf der Basis von regelmŠ§igen Vielecken werden Sternfiguren konstruiert.
2 Strecke
†ber einer Strecke, die wir als Zweieck interpretieren, zeichnen wir den Kreis des Thales und unten und oben je ein rechtwinkliges Dreieck. Diese rechtwinkligen Dreiecke setzen wir neu zusammen gemŠ§ Abbildung 1.
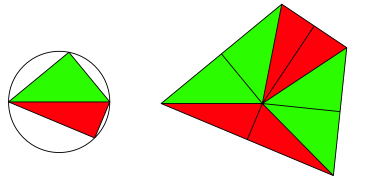
Abb. 1: Arrangement der rechtwinkligen Dreiecke
Es entsteht ein Viereck, das dem Titel Sternfigur wenig gerecht wird. Das Viereck hat einen Umkreis. Der Umkreisradius ist die Ausgangsstrecke. Die Diagonalen des Viereckes stehen orthogonal (Abb. 2). Dies lŠsst sich mit Winkelźberlegungen zeigen.
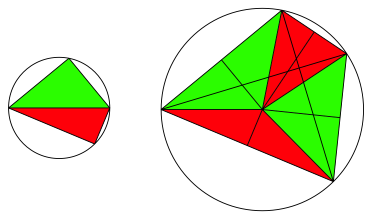
Abb. 2: Umkreis und orthogonale Diagonalen
3 Dreieck
Wir beginnen mit einem gleichseitigen Dreieck und setzen auf den Seiten Dreiecke mit einem Winkel von 120ˇ an. Die zu diesen Winkeln gehšrenden Ecken liegen auf dem Umkreis des Dreieckes. Nun setzen wir diese Dreiecke zu einem Stern zusammen (Abb. 3).
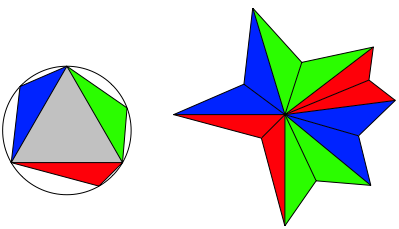
Abb.3: Sternfigur auf Dreiecksbasis
Die Spitzen des Sterns liegen auf einem Kreis. Der Radius dieses Kreises ist die SeitenlŠnge des gleichseitigen Dreieckes. Die Verbindungsstrecken diametraler Spitzen schneiden sich unter Winkeln von 60ˇ (Abb. 4). Dies lŠsst sich mit Winkelźberlegungen zeigen. Dazu studiert man die WinkelŠnderungen der Normalen dieser Verbindungstrecken.
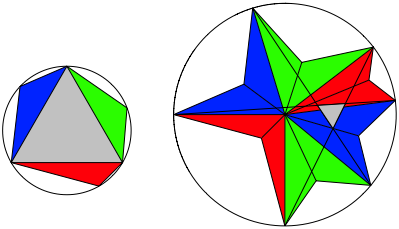
Abb. 4: Umkreis und Winkel von 60ˇ
4 Quadrat
Wir ersetzen das gleichseitige Dreieck durch ein Quadrat (Abb. 5). Die angesetzten Dreiecke haben nun Winkel von 135ˇ.
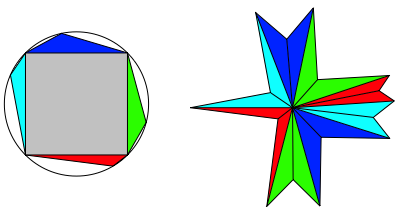
Abb. 5: Sternfigur auf Quadratbasis
Die Diagonalen der Sternfigur schneiden sich unter Winkeln von 45ˇ und Vielfachen davon (Abb. 6).
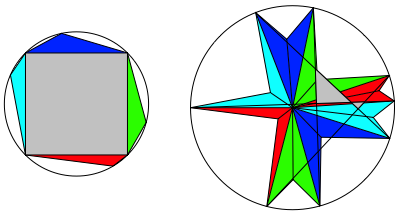
Abb. 6: Umkreis. Diagonalenwinkel 45ˇ und Vielfache
5 Pentagon
Die Abbildung 7 zeigt das Analoge fźr das Pentagon.
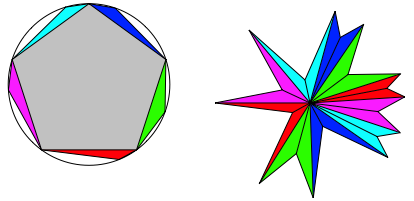
Abb. 7: Sternfigur auf Pentagonbasis
Die Diagonalen schneiden sich unter Winkeln von 36ˇ und Vielfachen davon (Abb. 8).
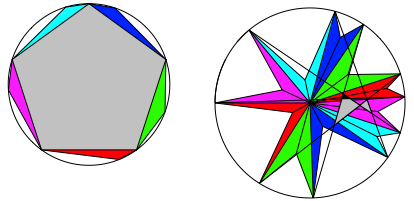
Abb.8: Umkreis und Diagonalen