Hans Walser, [20120829]
Sternparkett
1 Worum es geht
Es wird ein Parkett
besprochen, welches aus rechtwinklig-gleichschenkligen Dreiecken und Silbernen
Rechtecken besteht. Silberne Rechtecke haben das SeitenverhŠltnis ![]() .
.
2 Stern
Aus acht rechtwinklig-gleichschenkligen Dreiecken bauen wir einen Stern (Abb. 1).

Abb. 1: Stern
3 Stern-Parkett
Nun fźgen wir kongruente Sterne zusammen gemŠ§ Abbildung 2.

Abb. 2: Stern-Parkett
Wir sehen quadratische Lšcher und rechteckige Lšcher.
Die quadratischen Lšcher kšnnen je mit vier Dreiecken gefźllt werden, welche zu den rechtwinklig-gleichschenkligen Startdreiecken kongruent sind (Abb. 3). Die rechteckigen Lšcher sind Silberne Rechtecke.

Abb. 3: Quadrate und Silberne Rechtecke
4 Achtecke
Die Spitzen des ursprźnglichen Sterns bilden ein regelmŠ§iges Achteck. Es finden sich aber noch weitere regelmŠ§ige Achtecke, welche grš§er oder kleiner sind. In der Abbildung 4 sind Beispiele eingezeichnet.
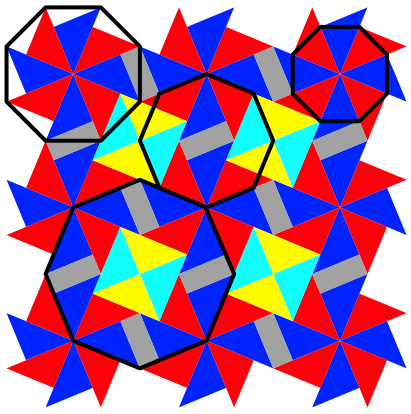
Abb. 4: RegelmŠ§ige Achtecke
5 Silberne Rechtecke
ZusŠtzlich zu den eingezeichneten Silbernen Rechtecken gibt es noch versteckte grš§ere Silberne Rechtecke (Abb. 5).

Abb. 5: Silberne Rechtecke