Hans Walser, [20201214]

Streifen, DIN-Rechteck und Goldenes Rechteck

1   Worum geht es?

Spielerei in einer Figur mit gleich breiten Streifen. Es erscheinen das DIN-Rechteck und ein mit dem Goldenen Rechteck verwandtes Rechteck.

2   Streifen

Wir arbeiten mit sechs gleich breiten Streifen und einem eingepassten Kreis (Abb. 1). Sein Radius ist das Dreifache der Streifenbreite.

Abb. 1: Streifen und Kreis

3   Rechtecke

Wir passen zwei Rechtecke ein (Abb. 2).

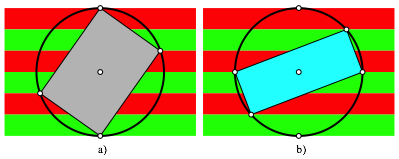
Abb. 2: Rechtecke

Das graue Rechteck der Abbildung 2a ist ein sogenanntes DIN-Rechteck. Es hat das SeitenverhŠltnis . Zum Beispiel hat ein DIN A4 Papier dieses SeitenverhŠltnis. †ber das DIN-Format siehe Walser 2013b.

Hintergrund und Beweisschlźssel:

 

                                                                                       (1)

 

 

 

 

Auf der linken Seite von (1) erscheint die zum DIN-Format gehšrende Zahl . Der Drittel in der rechten Seite entspricht einer Streifenbreite im VerhŠltnis zum Kreisradius. Der durch (1) definierte Winkel (etwa 70.5288ˇ) ist der Schnittwinkel der beiden Rechteckdiagonalen.

Das Rechteck der Abbildung 2b hat das SeitenverhŠltnis . Dabei ist

 

                                                                                                       (2)

 

 

 

 

der so genannte Goldene Schnitt (Walser 2013a).

Hintergrund und Beweisschlźssel:

 

                                                                                       (3)

 

 

 

 

Der durch (3) definierte Winkel (etwa 41.8103ˇ) ist der Schnittwinkel der Diagonalen des Rechtecks.

4   Das Goldene Rechteck

Unter dem Goldenen Rechteck versteht man das Rechteck mit dem SeitenverhŠltnis . Es gibt zwei Mšglichkeiten, vom Rechteck der Abbildung 2b zum Goldenen Rechtecke zu gelangen. Beide operieren mit einem Quadrat.

Wir kšnnen ein Quadrat abschneiden. Das Restreckteck ist ein Goldenes Rechteck (Abb. 3a).

Wir kšnnen zum Quadrat ergŠnzen. Das ErgŠnzungsrechteck ist ein Goldenes Rechteck (Abb. 3b).

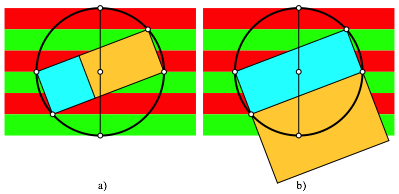
Abb. 3: Goldene Rechtecke

5   Im Dodekaeder

Die beiden Rechtecke der Abbildung 2 erscheinen auch im regulŠren Dodekaeder (Abb. 4).

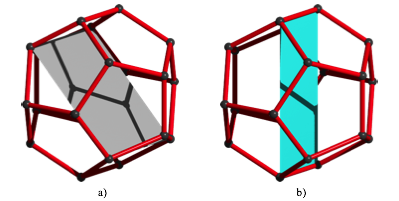
Abb. 6: Rechtecke im Dodekaeder

Literatur

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.