Hans Walser, [20180915]
Stumpf
1 Worum geht es?
Inhaltsformeln von ăStźmpfenŇ.
2 In der Ebene: Trapez als Dreieckstumpf
Wir sehen das Trapez als Differenz zweier Šhnlicher Dreiecke (Abb. 1).
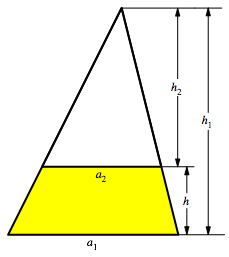
Abb. 1: Trapez
2.1 Erster Rechenweg
Wegen der €hnlichkeit der beiden Dreiecke ist:
![]() (1)
(1)
Fźr die TrapezflŠche ATrapez erhalten wir:
![]() (2)
(2)
Wegen (1) kšnnen wir eine rote Null hineinflicken:
 (3)
(3)
Wir erhalten die von der Schule her bekannte Formel.
2.2 Zweiter Rechenweg
Wegen der €hnlichkeit der beiden Dreiecke ist:
![]() (4)
(4)
Daraus folgt:
![]() (5)
(5)
In (2) eingesetzt liefert mit Hilfe der dritten binomischen Formel:
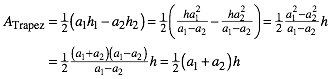 (6)
(6)
3 Im Raum: Kegel- oder Pyramidenstumpf
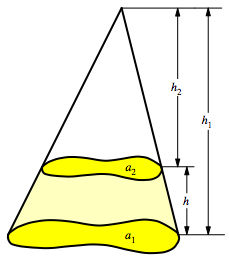
Abb. 2: Kegel- oder Pyramidenstumpf
Mit a1 und a2 bezeichnen wir nun die Boden- beziehungsweise die DeckflŠche. Es ist:
![]() (7)
(7)
Fźr das Volumen des Stumpfes erhalten wir:
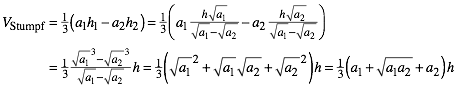 (8)
(8)
4 Im 4d-Raum
Wir erhalten analog fźr den 4d-Inhalt:
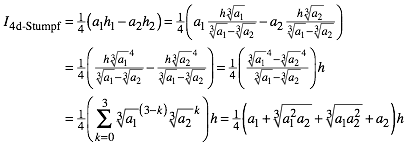 (9)
(9)
5 Im nd-Raum
Wir erhalten analog fźr den allgemeinen Fall:
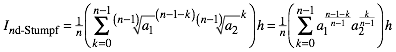 (10)
(10)
6 Mittelbildungen
6.1 Diskret
In unseren Beispielen erhielten wir fźr a1 und a2 die Mittelbildung:
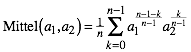 (11)
(11)
Fźr n = 2 ist dies das arithmetische Mittel.
Die Tabelle 1 zeigt die Mittel fźr a1 = 4 und a2 = 2 fźr n = 2, ... , 10.
|
n |
Mittel(4, 2) |
|
2 |
3 |
|
3 |
2.942809041 |
|
4 |
2.923661051 |
|
5 |
2.914085403 |
|
6 |
2.908341321 |
|
7 |
2.904512901 |
|
8 |
2.901778922 |
|
9 |
2.899728824 |
|
10 |
2.898134552 |
Tab. 1: Mittelbeispiele
Die Mittel werden kleiner. Gibt es eine untere Grenze bei wachsendem n?
6.2 Integral
Wir ersetzen die Summanden in (11) durch eine Funktion f wie folgt:
![]() (12)
(12)
Die Summe (11) ersetzen wir entsprechend durch ein Integral:
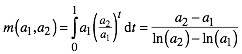 (13)
(13)
Fźr das Beispiel a1 = 4 und a2 = 2 (vgl. Tab. 1) erhalten wir:
![]() (14)
(14)