Hans Walser, [20200307]
Summe ungerader Zahlen
Idee und Anregung: M. S., B.
1 Worum geht es?
Visuelle Beweise fźr die Summenformel der erste n ungeraden Zahlen
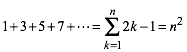 (1)
(1)
unter Verwendung eckiger Spiralen.
2 Aufbau der eckigen Spirale
Die Abbildungsfolge 1 zeigt den Aufbau der Spirale.
![]()
Abb. 1.1: Rechteck der LŠnge 1 (Quadrat)

Abb. 1.3: Rechteck der LŠnge 3 ansetzen
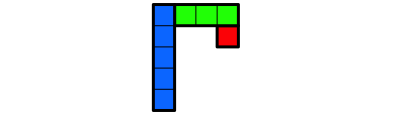
Abb. 1.5: Rechteck der LŠnge 5 ansetzen
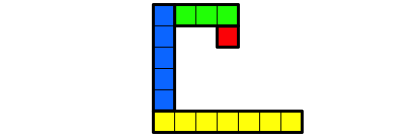
Abb. 1.7: Rechteck der LŠnge 7 ansetzen
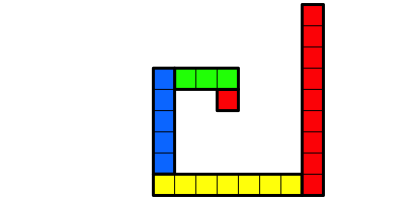
Abb. 1.9: Rechteck der LŠnge 9 ansetzen
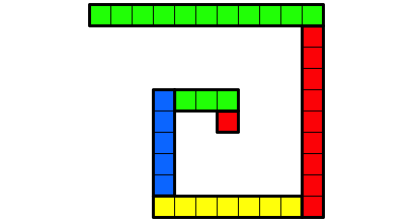
Abb. 1.11: Rechteck der LŠnge 11 ansetzen
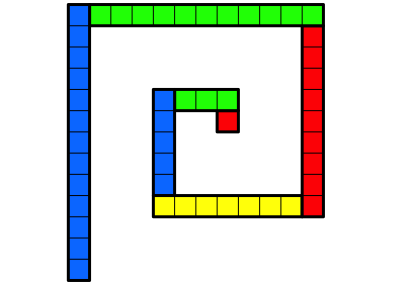
Abb. 1.13: Rechteck der LŠnge 13 ansetzen
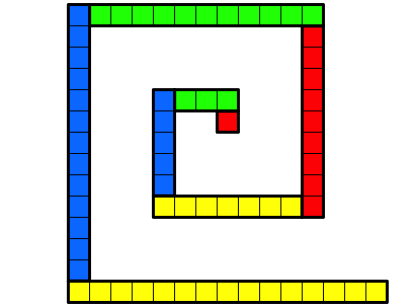
Abb. 1.15: Rechteck der LŠnge 15 ansetzen
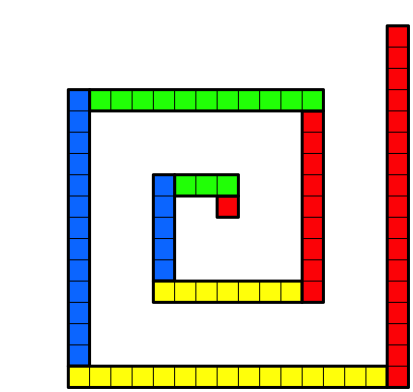
Abb. 1.17: Rechteck der LŠnge 17 ansetzen
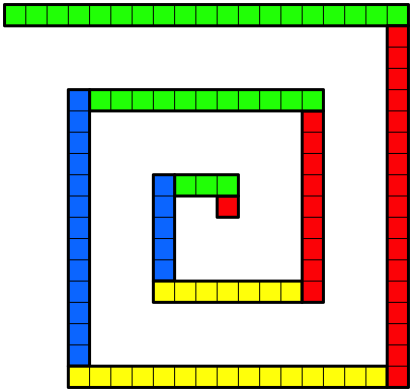
Abb. 1.19: Rechteck der LŠnge 19 ansetzen
Die Abbildung 2 zeigt die leere Spirale.

Abb. 2: Leere Spirale
3 Nummerierung
Nun nummerieren wir die quadratischen Felder von innen nach au§en, beginnend mit null (Abb. 3).

Abb. 3: Nummerierung
Wir haben an jeder Ecke eine Quadratzahl.
Wir markieren das jeweils mittlere Feld jedes Rechteckes (Abb. 4).
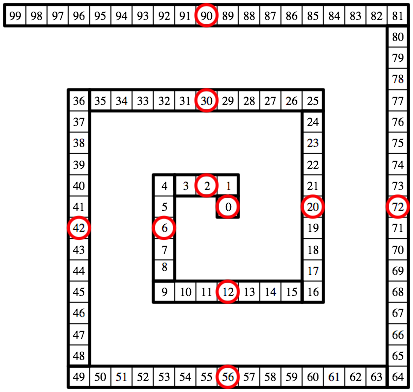
Abb. 4: Mittenfelder der Rechtecke
Die Zahlen in diesen Feldern sind gerade. Sie sind jeweils das geometrische Mittel der beiden benachbarten Quadratzahlen. Beispiel:
![]() (2)
(2)
Die Zahlen liegen auf vertikalen und horizontalen Linien (Abb. 5).
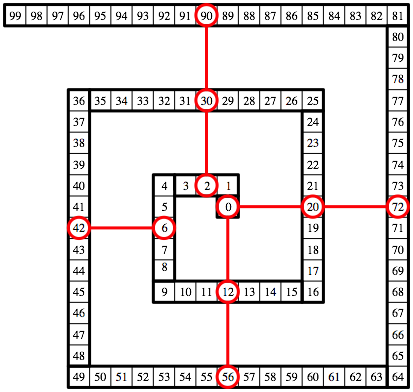
Abb. 5: Vertikale und horizontale Linien
4 Abknicken
Wir knicken nun in jedem der markierten Felder um 90ˇ. Aus den Rechtecken werden gleichschenklige rechte Winkel.
Damit erhalten wir die kompakte Spirale der Abbildung 6. Die Gesamtfigur ist ein Quadrat.
Es handelt sich dabei um die Ulam-Spirale, wobei die Nummerierung mit null beginnt.
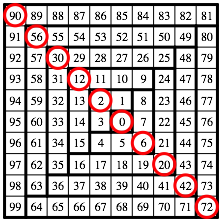
Abb. 6: Abgeknickt
Die Abbildung 7 zeigt dieselbe Figur ohne Zahlen. Wir erkennen die gleichschenkligen rechten Winkel.
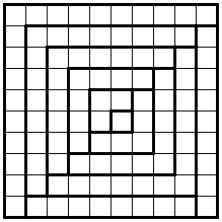
Abb. 7: Gleichschenklige rechte Winkel
In der Abbildung 8 sind diese Winkel farbig hervorgehoben. Jeder Winkel enthŠlt eine ungerade Anzahl von quadratischen Feldern.
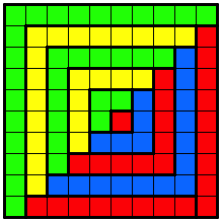
Abb. 8: Farbige Winkel
Websites
Hans Walser: Summe ungerader Zahlen
www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen/Ungerade_Zahlen.htm
Hans Walser: Summe ungerader Zahlen
www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen3/Summe_ungerader_Zahlen3.htm