Hans Walser, [20200320]

Summe ungerader Zahlen

1 Worum geht es?

Visueller Beweis für die Summenformel der erste n ungeraden Zahlen

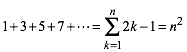(1)

2 Flache Treppe

Wir bilden Streifen aus den ersten n ungeraden Zahlen und schichten diese aufeinander (Abb. 1 für n = 8). Es entsteht eine flache Treppe.

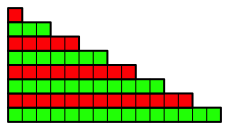
Abb.1: Streifen

3 Streifenmitten

In jedem Streifen markieren wir das mittlere Feld (Abb. 2).

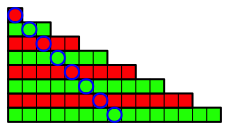
Abb. 2: Mittleres Feld

Die Markierungen laufen in einem Winkel von 45° nach unten.

4 Zum Winkel biegen

Nun biegen wir die zweite Streifenhälfte an der Markierung nach oben. Es entstehen gleichschenklige rechte Winkel.

Die Abbildungsfolge 3 zeigt das schrittweise Vorgehen.

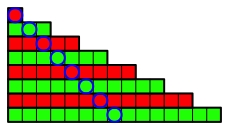
Abb. 3.1: Am Anfang gibt es nichts zu tun

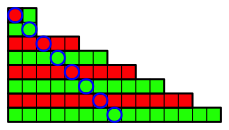
Abb. 3.2: Zweiter Schritt

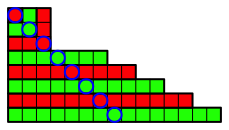
Abb. 3.3: Dritter Schritt

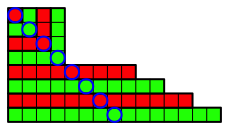
Abb. 3.4: Vierter Schritt

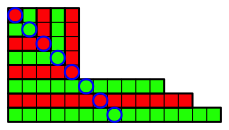
Abb. 3.5: Fünfter Schritt

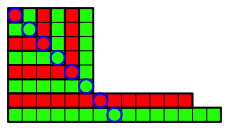
Abb. 3.6: Sechster Schritt

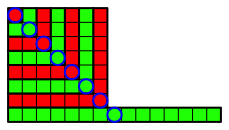
Abb. 3.7: Siebenter Schritt

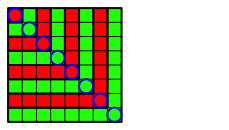
Abb. 3.8: Achter Schritt

Damit ist (1) gezeigt.

Websites

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen/Ungerade_Zahlen.htm