Hans Walser, [20200322]

Summe ungerader Zahlen

Idee und Anregung: Marc Sauerwein, Bonn

1 Worum geht es?

Visualisierung der Summenformel der ersten n ungeraden Zahlen:

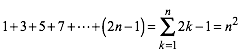(1)

Zur Visualisierung werden eckige Spiralen verwendet. Sie visualisieren den Fall n = 6.

2 Vier Spiralen

Die Abbildungsfolge 1 zeigt den Aufbau einer Spirale. Wir beginnen mit einem Quadrat.

Abb. 1.1: Startquadrat

Nun setzen wir quer einen Streifen mit drei Quadraten an.

Abb. 1.2: 1 + 3

Nun ein Streifen mit fünf Quadraten.

Abb. 1.3: 1 + 3 + 5

Und so weiter.

Abb. 1.4: 1 + 3 + 5 + 7

Abb. 1.5: 1 + 3 + 5 + 7 + 9

Abb. 1.6: 1 + 3 + 5 + 7 + 9 + 11

Es entsteht eine eckige Spirale. Die Anzahl der Quadrate ist gleich der Summe der n ersten ungeraden Zahlen. Der äußerste Schenkel hat die Länge 2n – 1.

Wir bauen nun vier solche Spiralen. Diese können wir ineinanderfügen (Abb. 2). Es entsteht ein großes Quadrat mit der Seitenlänge 2n.

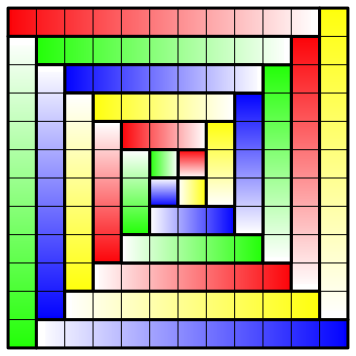
Abb. 2: Vier Spiralen

Das große Quadrat besteht also aus (2n)² = 4n² kleinen Quadraten. Für jede der vier Spiralen sind das n² kleine Quadrate. Damit ist (1) gezeigt.

3 Drei Spiralen

Die Startfigur besteht je nach Sichtweise aus einem Rhombus mit dem Spitzenwinkel 60° oder aus einem Quadrat auf der Oberfläche eines Würfels.

Abb. 3.1: Startfigur

Wir setzen nun einen Streifen aus drei weiteren Rhomben oder aus drei Quadraten an.

Abb. 3.2: 1 + 3

Und so weiter.

Abb. 3.3: 1 + 3 + 5

Abb. 3.4: 1 + 3 + 5 + 7

Abb. 3.5: 1 + 3 + 5 + 7 + 9

Abb. 3.6: 1 + 3 + 5 + 7 + 9 +11

Es entsteht eine eckige Spirale. Die Anzahl der Quadrate ist gleich der Summe der n ersten ungeraden Zahlen.

Wir bauen nun drei solche Spiralen. Diese können wir ineinanderfügen (Abb. 4). Die drei Spiralen bedecken drei Seitenquadrate eines Würfels der Kantenlänge n.

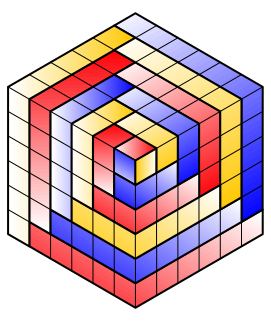
Abb. 4: Würfel

Die drei sichtbaren Seitenquadrate des großen Würfels enthalten insgesamt 3n² kleine Quadrate. Damit ist (1) gezeigt.

4 Fünf Spiralen

Es ist der Leserin oder dem Leser überlassen, wie ob sie oder er die Figur der Abbildung 5 als Folge von Rhomben mit dem Spitzenwinkel 72° oder als eine Ecke eines 5d-Hyperwürfels oder als eine Figur in der hyperbolischen Geometrie sehen will.

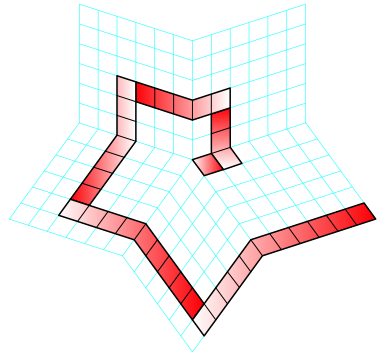
Abb. 5: Spirale

Fünf solche Spiralen (Abb. 6) führen wiederum zu einem Beweis von (1).

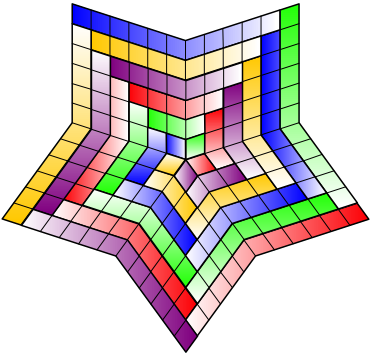
Abb. 6: Fünf Spiralen

Websites

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen/Ungerade_Zahlen.htm

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen2/Summe_ungerader_Zahlen2.htm

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen3/Summe_ungerader_Zahlen3.htm

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen5/Summe_ungerader_Zahlen5.htm