Hans Walser, [20200323]

Summe ungerader Zahlen

1 Worum geht es?

Visualisierung der Summenformel der ersten n ungeraden Zahlen

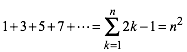(1)

Die folgenden Figuren basieren auf n = 7.

2 Sechseckraster

Wir beginnen mit einem regelmäßigen Sechseck (Abb. 1.1).

Abb. 1.1: 1

Dann setzen wir drei weitere Sechsecke an (Abb. 1.2).

Abb. 1.2: 1 + 3 = 4

Nun setzen wir fünf weitere Sechsecke an (Abb. 1.3).

Abb. 1.3: 1 + 3 + 5 = 9

Und so geht es weiter.

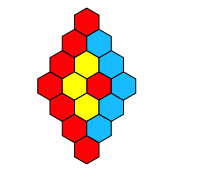
Abb. 1.4: 1 + 3 + 5 + 7 = 16

Abb. 1.5: 1 + 3 + 5 + 7 + 9 = 25

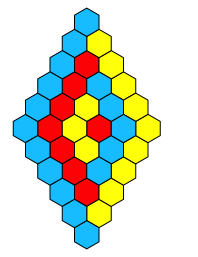
Abb. 1.6: 1 + 3 + 5 + 7 + 9 + 11 = 36

Abb. 1.7: 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49

3 Rhomben

Der Umriss ist ein Rhombus, der aus n schrägen Reihen von je n Sechsecken besteht. Wir haben also insgesamt n² Sechsecke. Damit ist (1) gezeigt.

4 Spiralen

Wir können gemäß dem Aufbau in der Abbildungsfolge 1 eine eckige Spirale einzeichnen (Abb. 2).

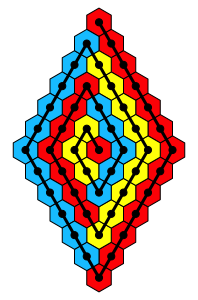
Abb. 2: Eckige Spirale

Wir können diese Spirale zu einer sogenannten Ulam-Spirale mit rechten Winkeln verzerren (Abb. 3). Der Umriss ist ein Quadrat.

Abb. 3: Ulam-Spirale

Die Abbildung 4 zeigt die Sechsecke ohne die Spirale.

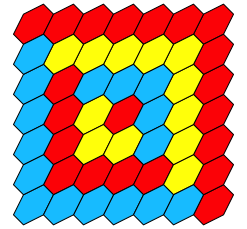
Abb. 4: Quadrat

5 Zahlen

Wir können gemäß der Spirale der Abbildung 2 die Sechsecke nummerieren, beginnend mit 1 im Zentrum (Abb. 5). Am Ende jeder Farbe ist jeweils eine Quadratzahl.

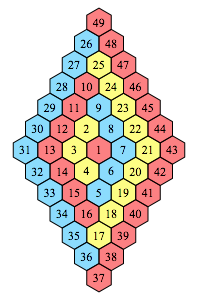
Abb. 5: Zahlen

Websites

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen/Ungerade_Zahlen.htm

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen2/Summe_ungerader_Zahlen2.htm

Hans Walser: Summe ungerader Zahlen

www.walser-h-m.ch/hans/Miniaturen/S/Summe_ungerader_Zahlen3/Summe_ungerader_Zahlen3.htm