Hans Walser, [20200515]
Summe von Potenzen
Aufgabenstellung: Thomas Jahre, Aufgabe 54-641_2
1 Die Aufgabe
Es gilt a + b = 1 und a² + b² = 2. Wie lautet das Ergebnis von a4 + b4 ?
2 Bearbeitung
ZunŠchst ist (quadratisches Problem):
(1)
Es sei 
. Die Tabelle 1 gibt die Werte fźr 
|
z |
sz |
|
–8 |
3104 |
|
–7 |
–1136 |
|
–6 |
416 |
|
–5 |
–152 |
|
–4 |
56 |
|
–3 |
–20 |
|
–2 |
8 |
|
–1 |
–2 |
|
0 |
2 |
|
1 |
1 |
|
2 |
2 |
|
3 |
5/2 |
|
4 |
7/2 |
|
5 |
19/4 |
|
6 |
13/2 |
|
7 |
71/8 |
|
8 |
97/8 |
Tab. 1: Einige Werte
Obwohl a und b irrational sind, sind sz rational, fźr negative Indizes z sogar ganzzahlig. Beim hŠndischen Ausrechnen (binomische Formel) sieht man das sofort ein.
3 Fibonacci
Die Folge
genźgt der
Rekursion
(2)
mit den
Stźtzwerten 
. Beweis induktiv.
Beispiele:
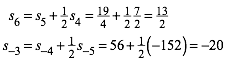(3)
Wir haben es also mit einer verallgemeinerten Fibonacci-Folge zu tun.
4 Wie ist es dazwischen?
Funktioniert
die Folge auch fźr nicht ganzzahlige Indizes? Was ist zum Beispiel 
? Da b
negativ ist, ergeben sich fźr 
komplexe
Werte.
So ist zum Beispiel:
(4)
Wir betrachten die Funktion:
(5)
Die
Abbildung 1 zeigt die komplexen Funktionswerte in der Gau§schen Ebene der
komplexen Zahlen fźr 
. Die Kurve verlŠuft gemŠ§ Tabelle 1 durch die reellen
Werte 2, 1, 2, 5/2, 7/2, 19/4.
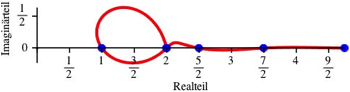
Abb. 1: Das SauschwŠnzlein
Die
Abbildung 2 zeigt die komplexen Funktionswerte fźr 
.
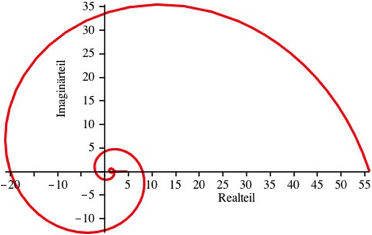
Abb. 2: AngenŠhert eine logarithmische Spirale
Wir erhalten approximativ eine logarithmische Spirale, welche aber nicht in den Ursprung einmźndet, sondern ins SauschwŠnzlein der Abbildung 1 źbergeht.
Website
Thomas Jahre, Aufgabe 54-641_2
https://www.schulmodell.eu/unterricht/faecher/mathematik/wochenaufgabe/serie-54.html?start=4