Hans Walser, [20210920]
Summen von Potenzen
0 Worum geht es?
Die Gleichung
![]() (1)
(1)
hat für n = 2 unendlich viele ganzzahlige Lösungen (pythagoreische Zahlentripel), hingegen für n > 2 keine (Fermat, Wiles).
Wir untersuchen ganzzahlige Lösungen der Gleichung:
![]() (2)
(2)
Vorgehen mit brute force.
1 Quadrate
|
a |
b |
c |
d |
Summe |
|
a |
b |
c |
d |
Summe |
|
1 |
7 |
5 |
5 |
50 |
|
3 |
16 |
11 |
12 |
265 |
|
1 |
8 |
4 |
7 |
65 |
|
3 |
19 |
9 |
17 |
370 |
|
1 |
12 |
8 |
9 |
145 |
|
4 |
13 |
8 |
11 |
185 |
|
1 |
13 |
7 |
11 |
170 |
|
4 |
17 |
7 |
16 |
305 |
|
1 |
17 |
11 |
13 |
290 |
|
4 |
18 |
12 |
14 |
340 |
|
1 |
18 |
6 |
17 |
325 |
|
4 |
19 |
11 |
16 |
377 |
|
1 |
18 |
10 |
15 |
325 |
|
5 |
14 |
10 |
11 |
221 |
|
2 |
9 |
6 |
7 |
85 |
|
5 |
15 |
9 |
13 |
250 |
|
2 |
11 |
5 |
10 |
125 |
|
5 |
20 |
8 |
19 |
425 |
|
2 |
14 |
10 |
10 |
200 |
|
5 |
20 |
13 |
16 |
425 |
|
2 |
16 |
8 |
14 |
260 |
|
6 |
17 |
10 |
15 |
325 |
|
2 |
19 |
13 |
14 |
365 |
|
7 |
17 |
13 |
13 |
338 |
|
3 |
11 |
7 |
9 |
130 |
|
7 |
19 |
11 |
17 |
410 |
|
3 |
14 |
6 |
13 |
205 |
|
8 |
19 |
13 |
16 |
425 |
Tab. 1: Quadrate
Lesebeispiel:
![]() (3)
(3)
2 Kuben
|
a |
b |
c |
d |
Summe |
|
1 |
12 |
9 |
10 |
1729 |
|
2 |
16 |
9 |
15 |
4104 |
|
2 |
24 |
18 |
20 |
13832 |
|
2 |
34 |
15 |
33 |
39312 |
|
3 |
36 |
27 |
30 |
46683 |
|
4 |
32 |
18 |
30 |
32832 |
|
9 |
34 |
16 |
33 |
40033 |
|
10 |
27 |
19 |
24 |
20683 |
|
12 |
40 |
31 |
33 |
65728 |
|
17 |
39 |
26 |
36 |
64232 |
Tab. 2: Kuben
Lesebeispiel:
![]() (4)
(4)
Das Beispiel (4) soll Ramanujan gegenüber Hardy erwähnt haben. Die Abbildung 1 illustriert den Sachverhalt.

Abb.
1: ![]()
Die Abbildung 2 zeigt nur die Würfel.
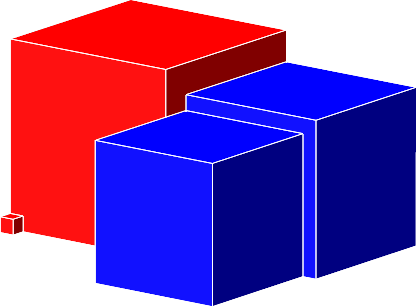
Abb. 2: Rot = blau
Die Abbildung 3 illustriert den Fall:
![]() (5)
(5)
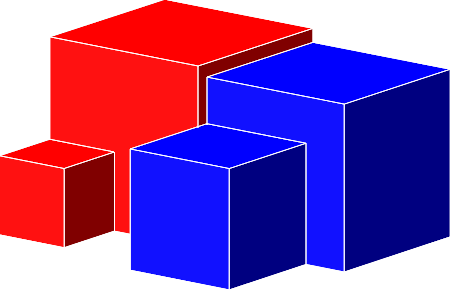
Abb. 3: Rot = blau
3 Vierte Potenzen
Es ist:
![]() (5)
(5)
Für weitere Lösungen stieß ich an die Kapazitätsgrenzen meines Computers. Analog für höhere Potenzen.