Hans Walser, [20121227]
Symmetrische Matrix
1 Die Matrix
Wir arbeiten mit der symmetrischen Matrix:
Eine symmetrische Matrix ist gleich ihrer
transponierten Matrix: 
2 Die Abbildung
2.1 Verzerrungsellipse
Wir verwenden die Matrix A als Abbildungsmatrix und bilden den Einheitskreis ab.
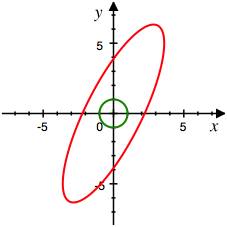
Bild des Einheitskreises
Der Kreis wird zu einer schrŠgen Ellipse verzerrt.
Wir sehen etwas mehr, wenn wir den Einheitskreis durch den Smiley ersetzen.
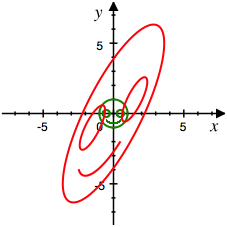
Smiley
2.2 Parameterdarstellung der Verzerrungsellipse
Der Einheitskreis hat die Parameterdarstellung:
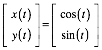
Nun multiplizieren wir mit der Matrix A:
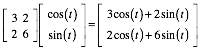
Rechts haben wir die Parameterdarstellung der Verzerrungsellipse.
Beim Smiley mŸssen die Augen und der Mund entsprechend bearbeitet werden.
2.3 Implizite Gleichung der Verzerrungsellipse
Wir mŸssen mit der
inversen Matrix 
arbeiten:
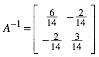
Nun setzen wir die Norm
von 
, also:
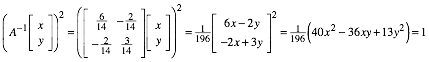
Die Idee ist, dass die
RŸckabbildung in den Einheitskreis 
passt.
Die Abbildung zeigt die Situation in dieser impliziten Darstellung. FŸrs Auge natŸrlich kein Unterschied zur obigen Parameterdarstellung.
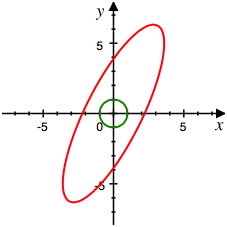
Implizite Darstellung
3 Eigenwerte und Eigenvektoren
Wir bestimmen die
Eigenwerte und Eigenvektoren der symmetrischen Matrix A: Wir erhalten die charakteristische Gleichung 
mit den beiden
Lšsungen 
und 
. Dies sind die Eigenwerte der Matrix A. FŸr die Eigenvektoren erhalten wir zum Beispiel:
und 
Die beiden Eigenvektoren sind orthogonal.
Allgemein gilt (ohne Beweis):
Eine symmetrische Matrix hat orthogonale Eigenvektoren.
Die Abbildung zeigt die beiden Eigenvektoren.
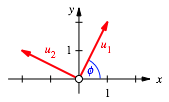
Eigenvektoren
Wir vermuten, dass der
Eigenvektor 
die Richtung der
langen Hauptachse (lange Symmetrieachse) der obigen Verzerrungsellipse hat. Der
Eigenvektor 
hat die Richtung
der kurzen Hauptachse (kurze Symmetrieachse) der Verzerrungsellipse.
FŸr den eingezeichneten
Winkel 
ergibt sich:
4 Eine Diagonalmatrix
Die Matrix
enthŠlt die Eigenwerte der Matrix A in der Diagonalen und sonst nichts. Die zugehšrige Abbildung ist eine Streckung in der x-Richtung um den Faktor 7 und in der y-Richtung um den Faktor 2. Der Einheitskreis wird zu einer Ellipse mit den Hauptachsen 7 und 2 verzerrt.
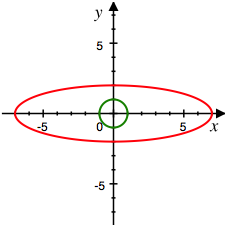
Verzerrung
Das ist offenbar wieder
unsere Verzerrungsellipse, aber um den Winkel 
zurŸckgedreht.
5 Noch eine Matrix
5.1 Eine Drehmatrix
Die Drehmatrix T fŸr den Winkel 
ist:
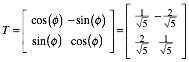
Diese Matrix hat folgende Eigenschaften:
Die Spaltenvektoren sind zueinander orthogonal.
Die Spaltenvektoren haben die LŠnge 1.
Die Spaltenvektoren (und ebenso die Zeilenvektoren) bilden also eine orthonormale Basis.
Es ist:
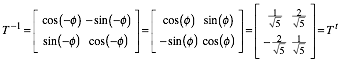
Eine Matrix mit diesen Eigenschaften wird als orthogonale Matrix bezeichnet.
5.2 Orthogonale Matrix
Quadratische Matrix Q mit folgenden Eigenschaften:
Die Spaltenvektoren sind zueinander orthogonal.
Die Spaltenvektoren haben die LŠnge 1.
Es ist 
.
Wir deine orthogonale Matrix als Abbildungsmatrix verwendet, bleiben LŠngen und Winkel invariant. Die Abbildung ist also eine Kongruenzabbildung. Die Abbildung ist eine Drehung oder eine Spiegelung.
Der entsprechende Begriff bei komplexen Matrizen ist die unitŠre Matrix.
6 Zusammensetzung von Abbildungen
Wir machen nun
folgendes: Wir drehen den Smiley um den Winkel 
zurŸck, dann verzerren
wir mit der Matrix 
, also in der x-Richtung
mit dem Faktor 7 und in der y-Richtung
mit dem Faktor 2, und dann drehen wir um den Winkel 
vorwŠrts. Dann
sollten wir dasselbe erhalten wie bei der Direktabbildung mit der Matrix A.
Die Figurenfolge zeigt, dass es klappt.
Zusammensetzung von Abbildungen
Wir sehen, dass der
erste Schritt, also das ZurŸckdrehen des Smileys um den Winkel 
, wesentlich ist und nicht Ÿbersprungen werden kann.
7 Vorgehen mit Matrizen
Dem Zusammensetzen von Abbildungen entspricht die Multiplikation von Matrizen.
GemŠ§ unseren †berlegungen muss gelten:
Kontrolle:
Die Sache ist also ok.
Umgekehrt gilt auch:
Eine symmetrische Matrix kann also ãdiagonalisiertÒ werden. In der Diagonalen stehen dann die Eigenwerte der Matrix.