Hans Walser, [20170313]
Symmetrie als Beweismittel
Idee und Anregung: E. V., M.
1 Worum geht es?
Es wird ein Satz der Elementargeometrie mit Hilfe der Symmetrieklassen fr Flchenornamente bewiesen.
2 Der Satz
Wir setzen den Seiten eines Sehnenvierecks Parallelogramme an (Abb. 1a). Die Parallelogramme sind jeweils aus zwei gegenberliegenden Seiten des Sehnenviereckes gebildet und haben alle denselben, aber beliebigen spitzen Winkel (kann auch ein rechter Winkel sein). Gegenberliegende Parallelogramme sind also kongruent, sozusagen ãHochformatÒ und ãQuerformatÒ.
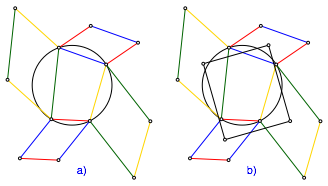
Abb. 1: Sehnenviereck und Parallelogramme
Satz: Die Zentren der Parallelogramme sind die Ecken eines Rechteckes.
3 Winkeleigenschaften
Im Sehnenviereck ergnzen sich gegenberliegende Winkel je auf 180¡. In den Parallelogrammen ergnzen sich spitze und stumpfe Winkel ebenfalls auf 180¡. Daher erscheinen die Innenwinkel des Sehnenvierecks au§en als Winkel zwischen den Parallelogrammen (Abb. 2a). Dabei wir die Orientierung umgedreht: der rote Winkel im Sehnenviereck hat als Schenkel im positiven Drehsinn die rote und die grne Seite des Sehnenviereckes, der rote Au§enwinkel hat dieselben Schenkel, aber im negativen Drehsinn.
Wir knnen daher zwischen die Parallelogramme spiegelbildliche (grne) Kopien des (gelben) Sehnenviereckes einfgen (Abb. 2b).
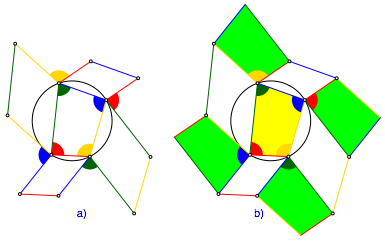
Abb. 2: Au§enwinkel
Die Abbildung 3 zeigt dasselbe wie die Abbildung 2b, zustzlich sind nun auch die Parallelogramme gefrbt.

Abb. 3: Farbige Parallelogramme
4 Flchenornament
Die Figur der Abbildung 3 knnen wir zu einem Flchenornament ausbauen (Abb. 4).

Abb. 4: Flchenornament
5 Symmetrien
Das Flchenornament hat folgende Symmetrien (Abb. 5):
Drehungen um 180¡. Die Drehzentren sind die Mittelpunkte der Parallelogramme.
Schubspiegelungen mit Achsen in zwei verschiedenen Richtungen.
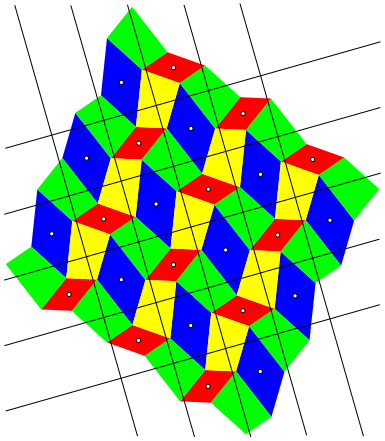
Abb. 5: Symmetrien
6 Symmetrieklassen
Bei Flchenornamenten gibt es 17 Symmetrieklassen [1] , [2] , [3] . Durchmustern der 17 Symmetrieklassen oder analytisches Vorgehen mit Hilfe der gegebenen Symmetrien zeigt, dass das Flchenornament zur Gruppe pgg gehrt. Diese Gruppe hat keine Symmetrieachsen, hingegen zwei zueinander senkrechte Schubspiegelachsen sowie zwei Klassen Drehzentren fr Drehungen von 180¡ (Punktspiegelungen).
7 Rechteckraster
Die Schubspiegelachsen bilden ein Rechteckraster. Aus Symmetriegrnden sind die Drehzentren (also die Mittelpunkte der Parallelogramme) die Mittelpunkte der einzelnen Rasterrechtecke. Diese Drehzentren sind die Eckpunkte des zum Rechteckraster der Schubspiegelachsen dualen Rasters und bilden daher ebenfalls ein Rechteckraster.
Damit ist der Satz bewiesen.
Fr den Beweis brauchten wir die Theorie der Symmetrieklassen der Flchenornamente. Diese Theorie wird also als Werkzeug eingesetzt.
Websites
[1] WallpaperPatterns (13.03.2017)
http://mathstat.slu.edu/escher/index.php/Wallpaper_Patterns
[2] Morandi, Patrick J. (2007): Symmetry Groups: The Classification of Wallpaper Patterns (13.03.2017)
http://sierra.nmsu.edu/morandi/OldWebPages/Math526Spring2007/Math526text2007-01-10.pdf
[3] Wikipedia: Ebene kristallographische Gruppe (13.03.2017)
https://de.wikipedia.org/wiki/Ebene_kristallographische_Gruppe