Hans Walser, [20150910]

Tangentenviereck mit Münzen

1 Auslegeordnung

Wir legen vier Münzen so aus, dass jede Münze zwei andere Münzen berührt (Abb. 1a).

Abb. 1: Vier Münzen

Die Zentren dieser vier Münzen bilden ein Tangentenviereck (Abb. 1b).

2 Beweis

Wir bezeichnen mit die Mittelpunkte der vier Münzen und entsprechend mit die Radien der vier Münzen (Abb. 2).

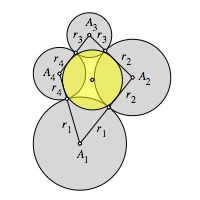
Abb. 2: Bezeichnungen

Dann ist:

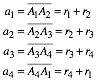(1)

Daraus ergibt sich:

(2)

Wir haben also das Kriterium für ein Tangentenviereck:

(3)

3 Berührungspunkte

Die Berührungspunkte der Münzen liegen zwar auf den Seiten des Tangentenviereckes, sind aber in der Regel nicht die Berührungspunkte des Inkreises (Abb. 3). Hingegen sind die Abstände zwischen diesen Punkten immer gleich groß und wechselseitig orientiert.

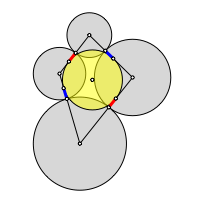
Abb. 3: Abstände