Hans Walser, [20150830]

Tangentenviereck als Gelenkmodell

Anregung: W. G., B und Chr. K., B.

1 Das Gelenkmodell

Die Abbildung 1 zeigt zwei Positionen eines Gelenkmodells für ein Tangentenviereck. Die jeweiligen Inkreise wurden nachträglich eingezeichnet.

Abb. 1: Tangentenviereck

2 Tangentenviereck

Ein Viereck mit den Seiten a, b, c, d ist genau dann ein Tangentenviereck, wenn gilt:

(1)

Das kann mit Tangentenabschnitten eingesehen werden. Oft wird der halbe Umfang einer Figur mit s bezeichnet. Im Falle eines Tangentenviereckes ist dann:

(2)

Die Bedingung (1) kann auch in der Form

(3)

geschrieben werden. In Worten: Die alternierende Seitensumme ist null.

Eine weitere Form ist die Differenzenform:

(4)

Im Beispiel der Abbildung 1 ist a = 10, b = 8, c = 5 und d = 7. Als Maßeinheit dient der Lochabstand.

Ein Viereck ist durch seine vier Seiten aber noch nicht festgelegt. Zu gegebenen vier Seitenlängen mit der Bedingung (1) gibt es also unendlich viele Tangentenvierecke. Dies legt die Idee des Gelenkmodells nahe dessen Seiten die Bedingung (1) erfüllen. In jeder Position erhalten wir ein Tangentenviereck. Die Größe des jeweiligen Inkreises variiert aber.

3 Nicht konvexes Tangentenviereck

Die Abbildung 2a zeigt nochmals das Gelenkmodell mit a = 10, b = 8, c = 5 und d = 7, aber die beiden kürzesten Seiten sind zusätzlich nach außen verlängert.

Abb. 2: Nicht konvex

Dieses Gelenkmodell kann in eine nicht konvexe Position gebracht werden (Abb. 2b). Es hat dann immer noch einen Inkreis, der aber teilweise die nun nach innen verlaufenden Verlängerungen der Seiten berührt.

4 Optimierung

4.1 Sehnenviereck

Man kann sich nun fragen, in welcher Position das Tangentenviereck mit gegebenen Seiten den größten Inkreis hat. Dies ist gleichbedeutend mit der Frage nach dem größten Flächeninhalt.

Allgemein hat ein beliebiges Viereck mit gegebenen Seitenlängen den größten Flächeninhalt in der Position des Sehnenviereckes (isoperimetrisches Problem für Vierecke). Beweis mit Differentialrechnung [1], [2]. Ein elementargeometrischer Beweis ist mir nicht bekannt.

Somit hat ein Tangentenviereck dann den größten Inkreis, wenn es auch ein Sehnenviereck ist.

4.2 Differenzialrechnung

Wir können die Optimierung des Tangentenvierecks aber auch ohne Bezugnahme auf das Sehnenviereck bearbeiten. Dazu arbeiten wir mit den Bezeichnungen der Abbildung 3.

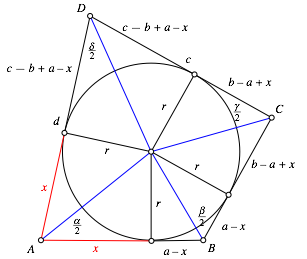
Abb. 3: Bezeichnungen

Zunächst ist:

(5)

Die Summe der halben Innenwinkel ist gleich :

(6)

Diese Gleichung (6) können wir mit CAS (Maple) nach r auflösen und erhalten so die Funktion deren Maximum wir nach dem üblichen Verfahren finden:

restart:

glg:= arctan(r/x)+arctan(r/(a-x))+arctan(r/(b-a+x))+arctan(r/(c-b+a-x))=Pi;

sol:=solve(glg, r):

r=sol[1];

r:=x->sqrt(-(a+c)*(a^3-2*a^2*b+a^2*c-2*a^2*x+a*b^2-a*b*c+2*a*b*x-2*a*c*x+a*x^2+c*x^2))/(a+c):

xmax:=solve(diff(r(x), x)=0, x);

rmax:=simplify(r(xmax));

Flaechemax:=simplify((a+c)*rmax);

Wir erhalten:

Abb. 4: Ergebnisse

Wegen (1) und (2) ist:

(7)

(8)

(9)

Mit diesen Angaben ist das optimale Tangentenviereck mit Zirkel und Lineal konstruierbar.

4.3 Konstruktion mit Zirkel und Lineal

Zu gegebenen Seiten a, b, c, d mit der Tangentenviereckbedingung (1) konstruieren wir zunächst in einer Nebenkonstruktion und und anschließend das optimale Tangentenviereck.

Die Nebenkonstruktionen verlaufen in einem Quadrat der Seitenlänge . Wir zeichnen dieses Quadrat und tragen auf der Deckgeraden die Strecken a und c sowie auf der Bodengeraden die Strecken b und d ab (Abb. 5). Die Abbildung 5a zeigt die Konstruktion von mit Hilfe des Strahlensatzes. Die Konstruktionsreihenfolge ist: schwarz (gegebene Daten), blau, grün, zyan, rot. Die Abbildung 5b zeigt die Konstruktion von . Verwendet werden dabei der Höhensatz im rechtwinkligen Dreieck und der Strahlensatz.

Die Daten für a, b, c, d entsprechen dem Modell der Abbildung 1.

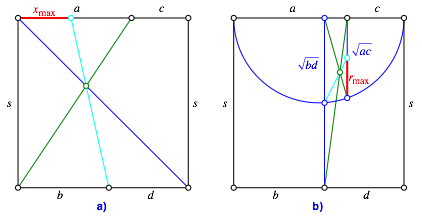
Abb. 5: Nebenkonstruktionen

Nun zeichnen wir die Strecke und unter Verwendung von und den Inkreis (Abb. 6a). Dann können wir zum gesuchten optimalen Tangentenviereck ergänzen (Abb. 6b).

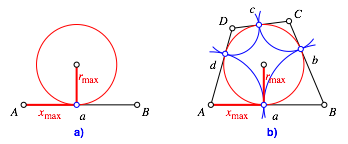
Abb. 6: Das optimale Tangentenviereck

4.4 Stülplösung

Wir können das Gelenkmodell der Abbildung 1 über einen Kegel stülpen (Abb. 7). Wenn das Gelenkmodell festsitzt, hat es die optimale Position.

Abb. 7: Stülplösung

5 Sonderfälle

Das Gelenkmodell der Abbildung 1 kann auf zwei Arten zu einem Dreieck gestreckt werden (Abb. 8).

Abb. 8: Zum Dreieck gestreckt

Der Inkreis berührt dann die gestreckte Seite genau im „gestreckten Eckpunkt“ also im Gelenkpunkt in welchem die beiden anschließenden Viereckseiten einen Winkel von 180° einschließen. Dies folgt aus (1) sowie dem Sachverhalt, dass in einem Dreieck der Tangentenabschnitt von einer Ecke zum Berührungspunkt des Inkreises gleich der Differenz des halben Umfanges und der gegenüberliegenden Seitenlänge ist.

Einfacher ist eine dynamische Überlegung: Das Gelenkmodell hat ja in jeder Position einen Inkreis, also auch bei Annäherung an die Sonderfallposition des Dreieckes. Die Tangentenabschnitte auf den vom zu streckenden Eckpunkt ausgehenden Seiten gehen dabei gegen Null. Also fallen die beiden auf diesen Seiten liegenden Berührungspunkte zusammen und sind mit dem gestreckten Eckpunkt identisch.

Auch die beiden anderen Berührungspunkte des Inkreises mit den Dreiecksseiten sind ganzzahlig. Dies folgt trivialerweise aus der „Ganzzahligkeit“ unseres Modells.

Wird das Gelenkmodell eines beliebigen Vierecks zum Dreieck gestreckt haben wir keinen Berührungspunkt im gestreckten Eckpunkt. Die Abbildung 9 zeigt ein Gegenbeispiel mit a = 10, b = 8, c = 7 und d = 4. Die Bedingung (1) für das Tangentenviereck ist verletzt. Die Berührpunkte der Inkreise sind weit daneben.

Abb. 9: Gegenbeispiel. Kein Tangentenviereck

6 Kein „überschlagendes“ Tangentenviereck

Die Abbildung 10 zeigt ein „überschlagenes“ Viereck. Das Gelenkmodell in der Foto (Abb. 10b) ist allerdings kein Tangentenviereck, sondern das schon einmal (Abb. 9) verwendete Gegenbeispiel mit a = 10, b = 8, c = 7 und d = 4, wo die Bedingung (1) verletzt ist.

Abb. 10: Überschlagenes Viereck. Kein Tangentenviereck

Tatsächlich gibt es kein überschlagenes Viereck, das die Bedingung (1) für ein Tangentenviereck erfüllt.

Für den Beweis arbeiten wir mit den Bezeichnungen der Abbildung 10a. Aus der Dreiecksungleichung für die beiden Dreiecke mit dem Kreuzungspunkt als einem gemeinsamen Eckpunkt ergibt sich:

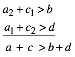(10)

Das widerspricht der Bedingung (1).

Auf diesen Sachverhalt ist der Autor gestoßen, als er versuchte, aus dem Gelenkmodell für das Tangentenviereck der Abbildung 1 ein überschlagenes Viereck zu machen. Dabei fand er auch die folgende Klappviereckeigenschaft.

7 Klappviereck

Das Gelenkmodell eines Tangentenviereckes lässt sich zusammenklappen wie ein Taschenmesser (Abb. 11). Das zusammengeklappte Viereck ist so lang wie die längste Viereckseite.

Abb. 11: Klappviereck

Genau die Tangentenvierecke sind Klappvierecke. Dies folgt aus (4) und der Struktur des zusammengeklappten Modells.

Für den Fall des Rhombus funktioniert das Zusammenklappen nur, wenn wir die Gelenkbreite vernachlässigen.

8 Plattdrücken eines geschlossenen Bandes

Wir bauen nun ein Gelenkmodell eines Tangentenviereckes auf der Basis des Klappviereckes. Dazu kleben wir einen Papierstreifen zu einem geschlossenen Band zusammen (Abb. 12). Dieses Band drücken wir nun flach und zwar so, dass insgesamt vier Faltlinien quer zum Streifen entstehen. Damit ergibt sich ein Gelenkmodell eines Tangentenviereckes, weil sich die Bedingung (4) von selber einstellt. Die Papierstreifen haben eine Tendenz, sich nicht im Sinne des Erfinders zu krümmen.

Abb. 12: Flachdrücken des geschlossenen Bandes

9 Modell aus Kartonstreifen

Die Abbildung 13 zeigt eine weitere Art eines Gelenkmodells für ein Tangentenviereck, inspiriert durch das Modell der Abbildung 12. Dazu schneiden wir von einem eher starken Karton zwei gleich breite und gleich lange Streifen ab, den einen für a + c und den anderen für b + d. Diese Streifen zerschneiden wir beliebig in je zwei Teile und erhalten so die Seiten a, b, c, d. Die Gelenke bauen wir mit beidseitig angebrachten Klebebändern.

Abb. 13: Gelenkmodelle aus Kartonstreifen

Dieses Modell lässt sich auch im Fall des Rhombus zusammenklappen. Einigermaßen wenigstens.

10 Idealisieren und vernachlässigen

Mathematiker sind groß im Vernachlässigen und Idealisieren. Die Strecken im Gelenkmodell sind keine idealen Strecken. Sie haben eine gewisse Breite. Diese Breite wurde etwa in der Abbildung 10a gegenüber dem realen Modell der Abbildung 10b schlicht vernachlässigt.

In Beispiel der Abbildung 1 wurde die Breite der Lochstreifen nicht vernachlässigt. Der Inkreis wurde nicht für das ideale Viereck gezeichnet, sondern für das Innenprofil (was die Fensterbauer das Licht nennen). Nun ist es allerdings so, dass das keine Rolle spielt, solange die Streckenbreite (gedacht als Streifenbreite) überall die gleiche ist (Abb. 14). Das Innenprofil, das ideale Tangentenviereck und auch das Außenprofil haben je einen Inkreis. Diese drei Inkreise haben dasselbe Zentrum, ihre Radien differieren um die halbe Streifenbreite.

In der Abbildung 14a sind die Ecken auf Gehrung gezeichnet. Bei den meisten Metallbaukästen sind sie rund (Abb. 14b). Das hat aber keinen Einfluss auf den Inkreis des Außenprofils.

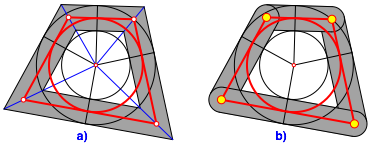
Abb. 14: Tangentenviereck mit Streifenbreite

Nebenbemerkung: Wir können die analoge Frage für Sehnenvierecke stellen. Da in einem Sehnenviereck die Summe gegenüberliegender Winkel je 180° ist, die Winkel bei Parallelstreifen sich aber nicht ändern, sind sowohl Innenprofil wie auch Außenprofil je ein Sehnenviereck. Wo liegen die Zentren der Umkreise?

11 Technisches

Wie ältere Semester schon lange festgestellt haben, sind die Gelenkmodelle der Abbildungen aus Lochstreifen aus Großvaters Metallbaukasten gebaut. Für die Gelenke wurde allerdings systemwidrig mit Mustertütenklammern gearbeitet. Das macht die Modelle zwar etwas wacklig, dafür tragen die Gelenke nur wenig auf.

Geht man im Modell der Abbildung 1 im positiven Sinn herum stellt man fest dass das jeweils folgende Lochband an drei Gelenkpunkten über das vorhergehende gelegt ist. Wir haben also dreimal „auf“. Am vierten Gelenkpunkt geht es dann stark hinunter. Der Niveauunterschied wurde beim vierten Gelenkpunkt mit mehreren Unterlagscheiben kompensiert. Vom ästhetischen Standpunkt aus ist das unbefriedigend. Die Lösung „auf-ab-auf-ab“ wäre viel ausgeglichener. Dann hätte aber das Klappviereck (Abb. 11) nicht funktioniert. Ein topologisches Problem.

12 Das Pappelproblem und eine didaktische Frage

Bei Metallbaukästen werden die Lochbänder nach der Lochzahl klassifiziert. In unserem Kontext ist aber die Anzahl der Lochabstände relevant. Diese ist um 1 kleiner als die Lochzahl. Allerdings macht es bei der Bedingung (1) nichts aus, wenn wir fälschlicherweise mit der Lochzahl arbeiten. Die Fehler kompensieren sich.

Die oben skizzierte Problematik taucht in vielen Beispielen im Unterricht auf. Oft ist es aber so, dass der Fehler sich nicht ausgleicht. Das klassische und abgegriffene Beispiel dazu ist die Frage nach der Länge einer Pappelallee, wenn die Anzahl der Pappeln und der Pappelabstand gegeben sind. Im Unterricht habe ich diesen Problemkreis etwas ironisch jeweils als „Pappelproblem“ bezeichnet. Mit dem Erfolg, dass eine Schülerin an der mündlichen Maturitätsprüfung in einem kombinatorischen Problem leise lächelnd sagte es handle sich hier um das Pappelproblem. Keine Pappel weit und breit.

Die Pappelaufgabe soll sicher nicht als Sachproblem oder als authentische Modellierungsaufgabe behandelt werden. Es geht darum, einem oft auftretenden Abzählproblem eine Ikone zu geben.

Wenn Sie in Ihrem Leben in n Wohnungen gelebt haben, wie oft sind Sie dann umgezogen?

Websites

[1] Flächenoptimierung im Viereck:

www.walser-h-m.ch/hans/Miniaturen/F/Fl_Opt_Viereck/Fl_Opt_Viereck.htm

[2] Isoperimetrische Vierecke mit gegebenen Seitenlängen:

www.walser-h-m.ch/hans/Miniaturen/I/Isoper_Vielecke/Isoper_Vielecke.htm