Hans Walser, [20120510]

Tangenten und Goldener Schnitt

Mit Hilfe von drei Kreisen und einer Tangente erhalten wir den Goldenen Schnitt. Es sind jeweils der Major blau und der Minor rot gezeichnet.

1 Konzentrische Kreise

Idee: T. W.

1.1 Situation

Wir zeichnen drei konzentrische Kreise mit dem Radienverhältnis und an den innersten Kreis eine Tangente gemäß Abbildung 1. Diese Tangente führt zum Goldenen Schnitt.

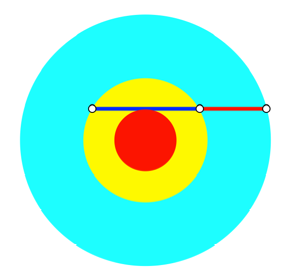
Abb. 1: Konzentrische Kreise und Tangente

1.2 Rechnerischer Beweis

Wir ergänzen die Figur gemäß Abbildung 2. Den Radius des innersten Kreises nennen wir r. Die beiden weiteren Kreise haben dann die Radien und .

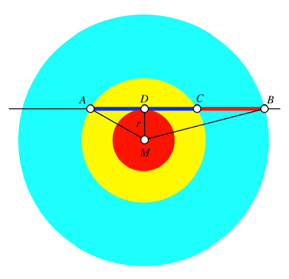
Abb. 2: Beweisfigur

Nach Pythagoras erhalten wir:

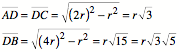
Damit wird:

Für das gesuchte Verhältnis ergibt sich:

Das ist das Verhältnis des Goldenen Schnittes, vgl. [Walser 2009].

1.3 Einbettung in die Figur von Odom

Wir können die Situation in die Figur von Odom einbetten (Abb. 3), in der sich ebenfalls der Goldene Schnitt ergibt [Walser 2009, S. 83].

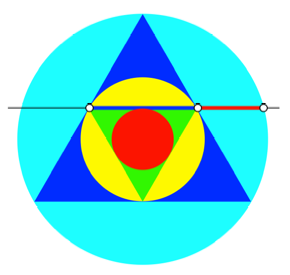
Abb. 3: Einbettung in die Figur von Odom

1.4 Einpassen in das Dreiecksfraktal

Die Figur kann auch mit dem Dreiecksfraktal [Walser 2009, S. 84] in Verbindung gebracht werden (Abb. 4).

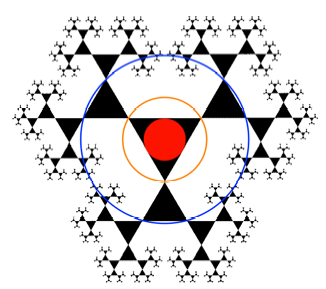
Abb. 4: Einpassen in das Dreiecksfraktal

2 Berührende Kreise

2.1 Erstes Beispiel

Wir zeichnen drei sich im selben Punkt berührende Kreise mit dem Durchmesserverhältnis sowie die zur Berührungstangente parallele andere Tangente an den kleinsten Kreis (Abb. 5). Wir erhalten wiederum den Goldenen Schnitt

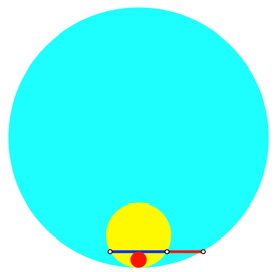
Abb. 5: Berührende Kreise

Für den Beweis ergänzen wir gemäß Abbildung 6. Der kleinste Kreis habe den Durchmesser d.

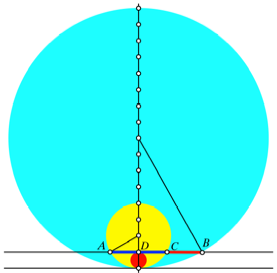
Abb. 6: Beweisfigur

Es ist dann:

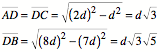
Damit wird:

Für das gesuchte Verhältnis ergibt sich:

Das ist das Verhältnis des Goldenen Schnittes.

2.2 Zweites Beispiel

Wir arbeiten analog mit dem Durchmesserverhältnis (Abb. 7).

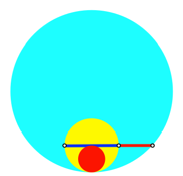
Abb. 7: Berührende Kreise

Für den Beweis ergänzen wir gemäß Abbildung 8. Der kleinste Kreis habe den Durchmesser d.

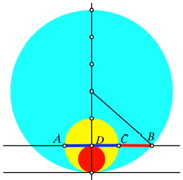
Abb. 8: Beweisfigur

Es ist:

Damit wird:

Für das gesuchte Verhältnis ergibt sich:

2.3 Berührung von außen

Wir zeichnen drei Kreise mit dem Radienverhältnis , die sich paarweise von außen berühren (Abb. 9). Die Berührungstangente der beiden großen Kreise führt zum Goldenen Schnitt.

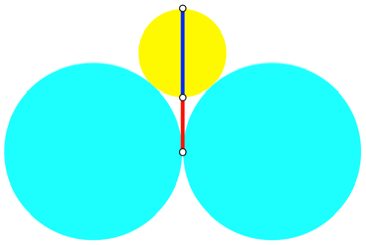
Abb. 9: Berührung von außen

Für den Beweis ergänzen wir die Figur gemäß Abbildung 10. Der kleine Kreis habe den Radius r.

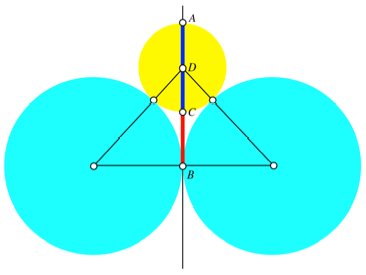
Abb. 10: Beweisfigur

Es ist:

Damit wird:

Für das gesuchte Verhältnis ergibt sich:

Das ist wiederum das Verhältnis des Goldenen Schnittes. Die Rechenschritte sind im Prinzip dieselben wie beim vorangegangenen Beispiel.

Literatur

[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1