Hans Walser, [20150915]

Tangententetraeder

1 Worum geht es?

In einem Tangententetraeder ist jede der sechs Kanten tangential an dieselbe Kugel. In einem Tangententetraeder ist die Summe der Längen gegenüberliegender Kanten invariant.

2 Kantenkugel

Jedes Tetraeder hat eine Umkugel und eine Inkugel. Das reguläre Tetraeder hat aber auch eine Kugel, welche sämtliche Kanten berührt (innere Kantenkugel, Abb. 1).

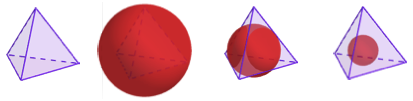
Abb. 1: Tetraeder mit Umkugel, innere Kantenkugel, Inkugel

Für ein Tetraeder der Kantenlänge 1 ergeben sich:

(1)

Ein reguläres Tetraeder hat noch vier weitere Kugeln, welche drei Kanten (die ein Seitendreieck bilden) und die Verlängerungen der drei anderen Kanten berühren. Die Abbildung 2 zeigt ein Beispiel. Die äußere Kantenkugel sitzt in einem Tetraederstumpf.

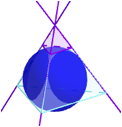
Abb. 2: Eine äußere Kantenkugel

3 Tetraeder ohne Kantenkugel

Nun hat aber nicht jedes Tetraeder eine (innere) Kantenkugel. Das Tetraeder der Abbildung 3 hat offensichtlich keine Kantenkugel.

Abb. 3: Keine Kantenkugel

Wir suchen Kriterien dafür, dass ein Tetraeder eine Kantenkugel hat.

4 Bedingung

Wir gehen von einem Tetraeder mit Kantenkugel aus und verwenden die Bezeichnungen der Abbildung 4. Die Färbung und Bezeichnung ist so gewählt, dass gegenüberliegende Tetraederkanten dieselbe Farbe und denselben lateinischen Bezeichnungsbuchstaben haben.

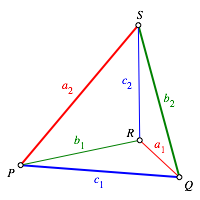
Abb. 4: Bezeichnungen

Mit x bezeichnen wir die drei von der Ecke X ausgehenden Tangentenabschnitte an die Kantenkugel. Die drei von einer Ecke ausgehenden Tangentenabschnitte sind alle gleich groß. Somit ist:

(2)

Daraus erhalten wir:

(3)

In Worten heißt das, dass die Summe gegenüberliegender Kantenlänge eine Konstante ist. Diese Konstante ist ein Drittel der integralen Kantenlänge. Die Bedingung (3) ist eine notwendige Bedingung für die Existenz eines Tangententetraeders. Um zu zeigen, dass sie auch hinreichend ist, benötigen wir einen Hilfssatz über das ebene Tangentenviereck.

5 Ein Satz im ebenen Tangentenviereck

Zunächst zerlegen wir ein beliebiges ebenes Viereck mit einer Diagonalen in zwei Dreiecke und zeichnen in jedem Teildreieck den Inkreis. Die beiden Inkreise berühren die Diagonale in der Regel in verschiedenen Punkten (Abb. 5). Man muss sich wieder klar machen, dass die Abbildungen 5 bis 7 ebene Figuren zeigen.

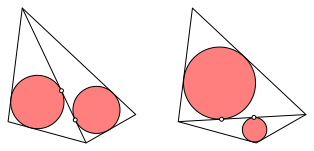
Abb. 5: Inkreise in Teildreiecken

Wir vermuten, dass die Distanz zwischen den beiden Berührungspunkten unabhängig davon ist, mit welcher Diagonale wir das Viereck unterteilt haben.

Zur Berechnung dieser Distanz verwenden wir die Bezeichnungen der Abbildung 6.

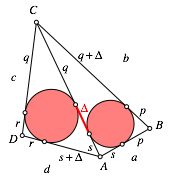
Abb. 6: Bezeichnungen

Wir berechnen die alternierende Seitensumme des Viereckes ABCD:

(4)

Somit ist:

(5)

Die Distanz ist also unabhängig von der zur Unterteilung gewählten Diagonale.

In einem Tangentenviereck ist nun die alternierende Seitensumme null. Daher ist auch , und die beiden Inkreise in den Teildreiecken haben den Berührungspunkt mit der Diagonalen gemeinsam (Abb. 7).

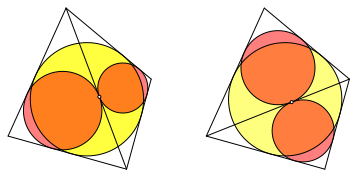
Abb. 7: Tangentenviereck

6 Abwicklung des Tetraeders

Die Abbildung 8 zeigt die Abwicklung eines Teteraeders, das die Bedingung (3) erfüllt. Bezeichnung und Farbe entsprechen der Abbildung 4. Die Spitze S kommt in der Abwicklung dreimal vor, als , und . Das Bodendreieck PQR liegt in der Mitte.

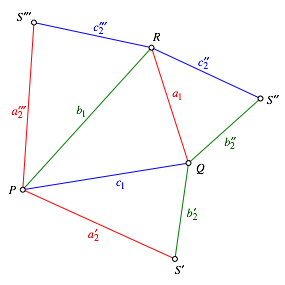
Abb. 8: Abwicklung

Wegen der Bedingung (3) ist das ebene Viereck ein Tangentenviereck. Es wird durch die Diagonale in zwei Dreiecke unterteilt. Gemäß dem Hilfssatz in Abschnitt 3 berühren sich die Inkreise der beiden Dreiecke auf (Abb. 9). Entsprechend überlegen wir für die weiteren in der Abbildung 9 eingezeichneten Kreise und Berührungspunkte. Wir haben nun für jedes Seitendreieck des Tetraeders den Inkreis.

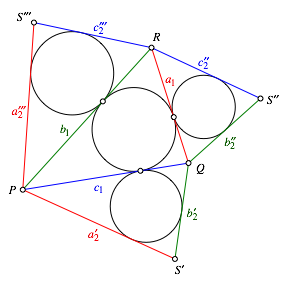
Abb. 9: Inkreise der Seitendreiecke des Tetraeders

Natürlich gilt das auch für die Berührungspunkte in den im Tetraeder „schrägen“ Tetraederkanten PS, QS und RS, welche in der Abbildung 9 wegen der Abwicklung zweimal gezeichnet sind (Abb. 10).

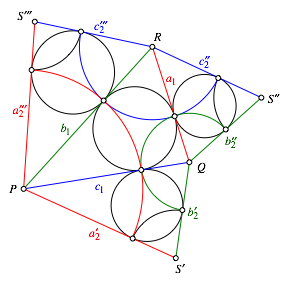
Abb. 10: Berührungspunkte auf den schrägen Kanten

Die Abbildung 11 zeigt die Situation im räumlichen Schrägbild auf dem Tisch ausgebreitet.

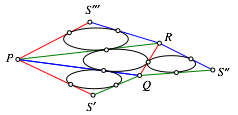
Abb. 11: Schräge Ansicht

So, und nun klappen wir die seitlichen Dreiecke hoch in den Raum. Da die Inkreise sich paarweise berühren, können wir genau eine Kugel einpassen, eben die Kantenkugel (Abb. 12).

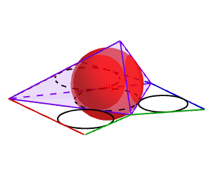
Abb. 12: Tetraeder mit innerer Kantenkugel

Es sei der Leserin überlassen, sich ein Schnittmuster für die außenliegenden Kantenkugeln zu machen.

7 Bemerkungen

7.1 Vergleich mit ebenem Tangentenviereck

Die Bedingung (3) für das Tangententetraeder entspricht der Bedingung für ein ebenes Tangentenviereck. Ein Tangentenviereck ist aber durch seine vier Seiten nicht fest gegeben. Die vier Seiten lassen ein Gelenkmodell zu. Das Tangententetraeder ist aber durch seine Kantenlänge bis auf Spiegelung eindeutig gegeben.

7.2 Tangentenvierecke in der Abwicklung

Werden zwei Seitendreiecke des Tangententetraeders mit gemeinsamer Kante in die Ebene abgewickelt, entsteht ein ebenes Tangentenviereck. Da wir sechs Kanten haben, gibt es sechs Möglichkeiten dazu. Die folgenden Abbildungen zeigen die sechs Möglichkeiten je mit Inkreis des Tangentenvierecks. Es sind pro Abbildung die beiden Möglichkeiten gezeichnet, die zu Gegenkanten des Tetraeders gehören. Der eine der beiden Inkreise wird zerschnitten dargestellt. Die beiden Kreissegmente sind im Regelfall keine Halbkreise.

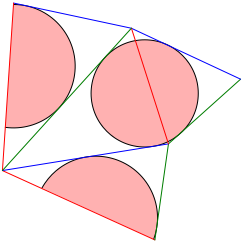
Abb. 13: Tangentenvierecke mit roter Diagonale

Abb. 14: Tangentenvierecke mit grüner Diagonale

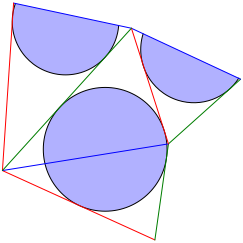
Abb. 15: Tangentenvierecke mit blauer Diagonale

Die Abbildung 16 zeigt die Überlagerung aller Möglichkeiten.

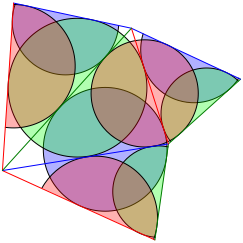
Abb. 16: Überlagerung

Obwohl es so aussieht, berühren sich die verschiedenen Inkreise im Regelfall nicht. Die Figur gibt also nicht so viel her wie man zuerst meint.