Hans Walser, [20230614]
Tangentenviereck
1 Worum geht es?
Konstruktion eines Tangentenviereckes aus den Winkelhalbierendenabschnitten.
2 Problemstellung
Von einem Tangentenviereck sind die vier Abschnitte von den Ecken zum Inkreismittelpunkt bekannt (Abb. 1). Gesucht ist das Tangentenviereck.
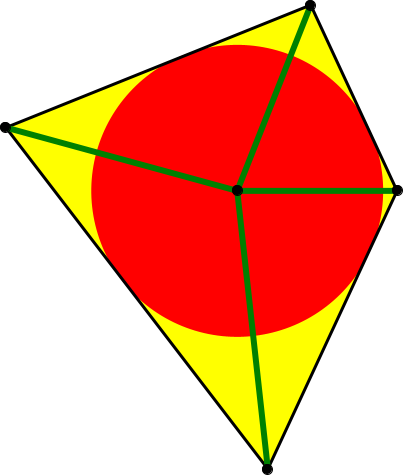
Abb. 1: Tangentenviereck
Im Beispiel der Abbildung 1 sind die vier Abschnitte auf den Winkelhalbierenden der Reihe nach 4, 5, 6, und 7. Es resultiert ein Inkreisradius r ≈ 3.627515540. Die Seitenlängen des Tangentenviereckes sind a ≈ 5.126659936, b ≈ 8.220334033, c ≈ 10.76598586, d ≈ 7.672311763. Wer Lust hat, kann nachprüfen, ob die alternierende Seitenlängensumme tatsächlich verschwindet.
3 Bearbeitung
Wir arbeiten mit den Bezeichnungen der Abbildung 2.
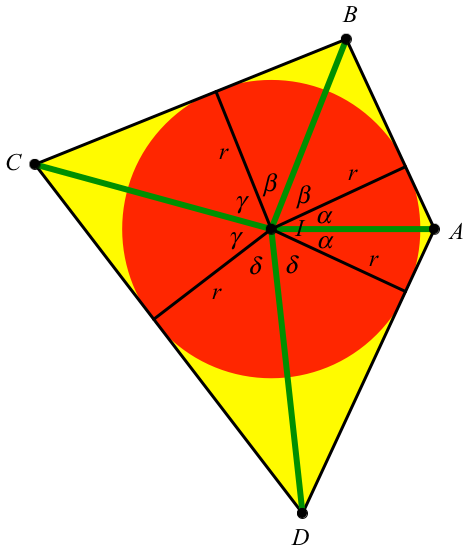
Abb. 2: Bezeichnungen
Es ist α = arccos(r/AI), β = arccos(r/BI), γ = arccos(r/CI), δ = arccos(r/DI). Wegen α + β + γ + δ = π ergibt sich für r die Gleichung:
arccos(r/AI) + arccos(r/BI) + arccos(r/CI) + arccos(r/DI) = π
Diese Gleichung lösen wir mit CAS.
4 Einschiebelösung
Die Abbildung 3 zeigt eine Einschiebelösung mit Aufblasen des Inkreises.
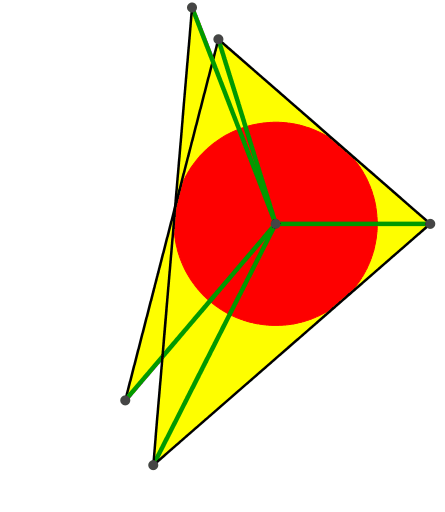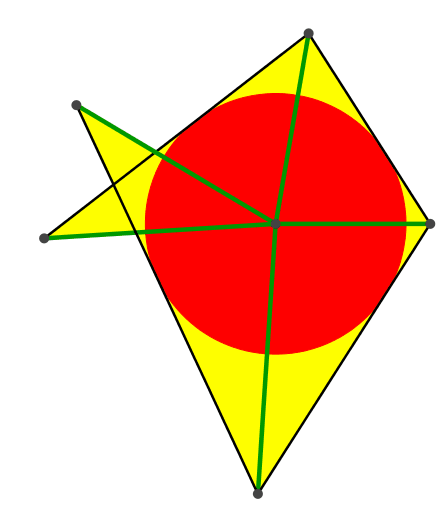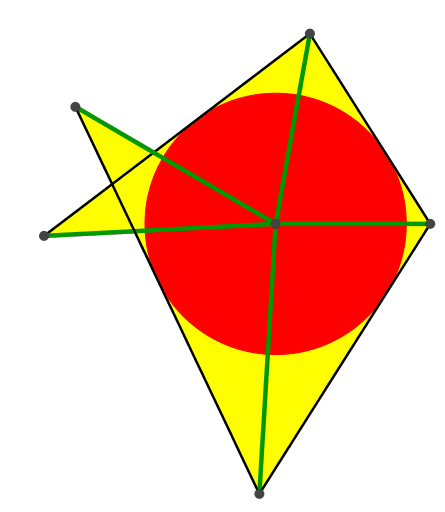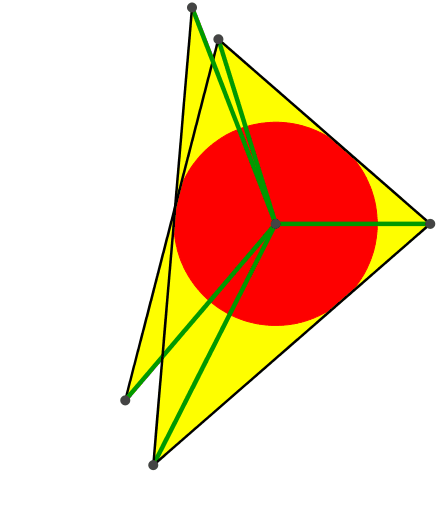
Abb. 3: Einschiebelösung
Weblinks
Hans Walser: Inkreismittelpunktabschnitte