Hans Walser, [20120729], [20131216]

Der Tante-Emma-Laden

1 Worum geht es?

In der Schule lernen wir, dass es Möglichkeiten gibt, aus einer Früchteschale mit n Früchten deren s auszuwählen. Dabei wird stillschweigend angenommen, dass alle Möglichkeiten gleichwertig sind. Dazu wird mit einem Urnenmodell gearbeitet, so dass blind ausgewählt werden muss.

Im Alltag ist es allerdings so, dass die besten Früchte zuerst vernascht werden.

2 Drei Personen

2.1 Vollzeit-Stellen

Im Tante-Emma-Laden arbeiten neben der Tante Emma (E) auch noch die Tanten Frieda (F) und Gertrud (G). Es sind immer zwei der drei Personen im Laden, die dritte hat frei.

Somit gibt es Möglichkeiten, eine Schichtbelegung mit zwei Personen zu finden, nämlich EF, EG und FG.

Wenn alle drei Personen vollzeit arbeiten, sind die drei Schichtbelegungen gleichwertig. Jede der drei Schichtbelegungen hat somit das Gewicht .

2.2 Unterschiedliche Stellenprozente

Nun sind aber die Anstellungsbedingungen unterschiedlich.

2.2.1 Beispiel

Tante	Stellenprozente	Faktor
Emma	e = 100%	e = 1
Frieda	f = 100%	f = 1
Gertrud	g = 50%	g = 1/2

Etwas Zahlenakrobatik:

· Wenn die drei Schichten EF, EG und FG alle gleiches Gewicht hätten, müsste Tante Gertrud gleich viel arbeiten wie die beiden anderen. Dies widerspricht ihren Anstellungsbedingungen.

· Die nahe liegende Idee ist natürlich, dass wir die Schicht EF doppelt so oft einsetzen wie die Schichten EG und FG (Gewicht 2 : 1 : 1). Dann arbeiten die Tanten Emma und Frieda in je drei Schichten, während die Tante Gertrud in zwei Schichten arbeitet. Sie arbeitet immer noch zu viel.

· Nun setzen wir die Schicht EF dreimal so oft ein wie die Schichten EG und FG (Gewicht 3 : 1 : 1). Dann arbeiten die Tanten Emma und Frieda in je vier Schichten, während die Tante Gertrud in zwei Schichten arbeitet. Dies entspricht den Anstellungsbedingungen.

Die drei Schichten haben also die Gewichte:

Schicht	Gewicht	Normiertes Gewicht
EF	3
EG	1
FG	1

Die Normierung bedeutet .

Die Frage ist, wie wir aus den gegebenen Daten e, f, g die Schichtgewichte x, y, z berechnen können.

2.2.2 Noch ein Beispiel

Nun arbeitet auch die Tante Frieda nur noch halbtags:

Tante	Stellenprozente	Faktor
Emma	e = 100%	e = 1
Frieda	f = 50%	f = 1/2
Gertrud	g = 50%	g = 1/2

Die geneigte Leserin ist eingeladen, sich die Sachlage durch den Kopf gehen zu lassen, bevor sie weiter liest.

Die Schicht FG kann gar nicht eingesetzt werden, weil sonst die Tante Emma in einen unaufholbaren Rückstand geraten würde. Die Tante Emma kann daher nie aus dem Laden.

Es sind also nur die Schichten EF und EG mit je gleichem Gewicht möglich:

Schicht	Gewicht	Normiertes Gewicht
EF	1
EG	1
FG	0

2.2.3 Etwas Mathematik

Die Frage ist, wie wir aus den gegebenen Anstellungsdaten e, f, g die Schichtgewichte x, y, z berechnen können.

In der Schicht EF (Gewicht x) Arbeiten die Tanten Emma und Frieda, in der Schicht EG (Gewicht y) die Tanten Emma und Gertrund und in der Schicht FG (Gewicht z) die Tanten Frieda und Gertrud.

Für die Arbeitszeit der Tante Emma sind also x und y relevant, für die Tante Frieda x und z und für die Tante Gertrud y und z. Damit die Arbeitszeiten in der richtigen Relation stehen, muss gelten:

Mit einem Proportionalitätsfaktor können wir das in folgender Form schreiben:

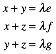
Jetzt haben wir ein lineares Gleichungssystem mit drei Gleichungen und den vier Unbekannten . Die Normierung liefert uns die noch benötigte vierte Gleichung.

Der Rest ist Rechnen.

2.2.4 Beispiele

In den Resultaten wird jeweils auch die technische Größe angegeben.

Erstes Beispiel (unser Einführungsbeispiel):

Anstellungsgrade:

e = 1, f = 1, g = 1/2

Schichtgewichte:

x = 3/5, y = 1/5, z = 1/5, lambda = 4/5

Zweites Beispiel (das zum Nachdenken, der Computer rechnet einfach):

Anstellungsgrade:

e = 1, f = 1/2, g = 1/2

Schichtgewichte:

x = 1/2, y = 1/2, z = 0, lambda = 1

Und noch ein drittes Beispiel (mit drei unterschiedlichen Anstellungsgraden):

Anstellungsgrade:

e = 1, f = 3/4, g = 1/2

Schichtgewichte:

x = 5/9, y = 1/3, z = 1/9, lambda = 8/9

Lauter Vollzeitstellen (die Gewichtung muss symmetrisch werden):

Anstellungsgrade:

e = 1, f = 1, g = 1

Schichtgewichte:

x = 1/3, y = 1/3, z = 1/3, lambda = 2/3

Interessant ist das folgende Beispiel:

Anstellungsgrade:

e = 1, f = 1/2, g = 1/4

Schichtgewichte:

x = 5/7, y = 3/7, z = —1/7, lambda = 8/7

2.3 Die Sache mit dem Rasenmäher

Der Tante-Emma-Laden übernimmt nun auch Rasenmäher ins Sortiment. Zur Beratung der Kunden muss das Personal entsprechend ausgebildet werden.

Man möchte einerseits möglichst eine ausgebildete Person in jeder Schicht haben und andererseits möglichst wenige Personen ausbilden.

· Wenn wir zwei der drei Tanten ausbilden, ist in jeder Schicht eine ausgebildete Person.

· Wenn wir nur eine Person ausbilden, ist es optimal, eine Person mit dem höchsten Anstellungsgrad auszubilden. Wenn das zum Beispiel die Tante Emma selber ist, erhalten wir für die Wahrscheinlichkeit, dass eine ausgebildete Person (eben die Tante Emma) im Laden ist:

Das Restrisiko, dass keine ausgebildete Person im Laden ist, beträgt demnach:

Beispiel:

Anstellungsgrade:

e = 1, f = 3/4, g = 1/2

Schichtgewichte:

x = 5/9, y = 1/3, z = 1/9, lambda = 8/9

Restrisiko = 1/9 = 0.1111

3 Vier Personen

Nun kommt noch der Onkel Hans (H) mit dem Arbeitsgrad h dazu.

3.1 Schichtgröße 2

Die Schichtgröße soll bei 2 bleiben. Es gibt verschiedene Schichten.

Schicht	Normiertes Gewicht
EF
EG
EH
FG
FH
GH

Wir haben die Bedingung:

Umgeschrieben und mit der Normierungsbedingung ergänzt:

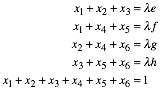
Das sind fünf Gleichungen für die sieben Unbekannten .

3.1.1 Unterbestimmtes System

Wenn wir naiv in den Computer gehen, erhalten wir zum Beispiel:

Anstellungsgrade:

e = 1, f = 1, g = 3/4, h = 1/2

Schichtgewichte:

x1 = 3/13+x6, x2 = 1/13+x5, x3 = 4/13-x5-x6,

x4 = 5/13-x5-x6, x5 = x5, x6 = x6, lambda = 8/13

Die Angaben und sind zwar absolut richtig, aber nicht informativ.

Das Gleichungssystem ist unterbestimmt, wir können zwei der sieben Unbekannten selber wählen. Die Schichtgewichtung ist also durch die Anstellungsgrade nicht festgelegt.

3.1.2 Beispiele

Wir wählen zum Beispiel und und erhalten:

Anstellungsgrade:

e = 1, f = 1, g = 3/4, h = 1/2

Schichtgewichte:

x1 = 49/156, x2 = 25/156, x3 = 11/78,

x4 = 17/78, x5 = 1/12, x6 = 1/12, lambda = 8/13

Mit und erhalten wir bei denselben Anstellungsgraden:

Anstellungsgrade:

e = 1, f = 1, g = 3/4, h = 1/2

Schichtgewichte:

x1 = 43/130, x2 = 21/104, x3 = 43/520,

x4 = 83/520, x5 = 1/8, x6 = 1/10, lambda = 8/13

Was ergibt sich bei lauter Vollzeitstellen?

Wenn wir und wählen, ergibt sich:

Anstellungsgrade:

e = 1, f = 1, g = 1, h = 1

Schichtgewichte:

x1 = 1/12, x2 = 1/12, x3 = 1/3,

x4 = 1/3, x5 = 1/12, x6 = 1/12, lambda = 1/2

Trotz gleichmäßiger Anstellungsgrade passt auch eine asymmetrische Schichtgewichtung.

Wenn wir und wählen, ergibt sich die erwartete symmetrische Verteilung:

Anstellungsgrade:

e = 1, f = 1, g = 1, h = 1

Schichtgewichte:

x1 = 1/6, x2 = 1/6, x3 = 1/6,

x4 = 1/6, x5 = 1/6, x6 = 1/6, lambda = 1/2

3.1.3 Wahrung des sozialen Friedens

Nehmen wir einmal an, die Tante Emma und Onkel Hans vertragen sich nicht so gut, und ebenso sind sich die Tante Gertrud und Onkel Hans nicht besonders grün. Das betrifft also die Schichten EH beziehungsweise GH mit den Gewichten und . Nun können wir und wählen und erhalten eine sozial verträgliche Schichtverteilung:

Anstellungsgrade:

e = 1, f = 1, g = 3/4, h = 1/2

Schichtgewichte:

x1 = 3/13, x2 = 5/13, x3 = 0,

x4 = 1/13, x5 = 4/13, x6 = 0, lambda = 8/13

3.1.4 Rasenmäher und Restrisiko

· Wenn drei Personen ausgebildet sind, gibt es nur eine unausgebildete Person. Damit hat es in jeder Schicht mindestens eine ausgebildete Person.

· Werden genau die beiden Tanten Emma und Frieda ausgebildet, ist das Restrisiko, dass keine ausgebildete Person im Laden ist, . Wie wir gesehen haben, können wir aber die Sache so steuern, dass . Das Restrisiko kann also durch organisatorische Maßnahmen zu null gemacht werden, ohne dass die Anstellungsgrade verletzt werden.

· Wird nur die Tante Emma am Rasenmäher ausgebildet, ist das Restrisiko . Dies kann nicht zu Null gemacht werden.

3.2 Schichtgröße 3

Bei Schichtgröße 3 gibt es verschiedene Schichten:

Schicht	Normiertes Gewicht
EFG
EFH
EGH
FGH

Wir haben die Bedingung:

Also:

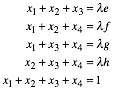
Das sind fünf Gleichungen für die fünf Unbekannten . Damit ist das Gleichungssystem eindeutig bestimmt.

3.2.1 Beispiel

Anstellungsgrade:

e = 1, f = 1, g = 3/4, h = 1/2

Schichtgewichte:

x1 = 7/13, x2 = 4/13, x3 = 1/13, x4 = 1/13,

lambda = 12/13

Rasenmäher und Restrisiko:

· Werden zwei Personen ausgebildet, gibt es in jeder Schicht mindestens eine ausgebildete Person.

· Wir zum Beispiel nur die Tante Emma ausgebildet, ist das Restrisiko .

4 Allgemein

4.1 Bedingungen und Freiräume

Der Laden habe n Angestellte mit unterschiedlichen Anstellungsgraden und eine Schichtgröße s.

Es gibt einerseits Schichtkombinationen und daher ebenso viele Gewichtungsvariable . Zusammen mit haben wir Variable.

Andererseits müssen n Anstellungsgrade sowie die Normierungsbedingung erfüllt sein, wir haben also Gleichungen.

Das entstehende lineare Gleichungssystem ist für und eindeutig bestimmt, für unterbestimmt. Wir können in diesem Fall Variable selber wählen. Damit haben wir im Hinblick auf das Rasenmäher-Problem viele Steuerungsmöglichkeiten.

4.2 Ein großer Laden

Ein Laden habe 44 Angestellte und die Schichtgröße 6.

Es ist:

Somit haben wir 45 Gleichungen mit 7059053 Unbekannten. Und wir haben 7059008 freie Variable.

5 Zusammenfassung

Das kombinatorische Urnenmodell setzt gleiche Anstellungsgrade voraus und liefert die gleichmäßige Lösung. Es gibt für unser Problem aber noch andere Lösungen.

Wir haben viele freie Parameter, die auch im Fall von ungleichen Anstellungsbedingungen anwendbar sind.

Die Gleichungssysteme sind linear, aber mit großen Datenmengen.

Das Rasenmäher-Problem kann optimiert werden. Dazu sind Methoden der linearen Optimierung zu verwenden. Grundsätzlich müssen Angestellte mit hohem Anstellungsgrad prioritär ausgebildet werden.