Hans Walser, [20181213]
Teilpunktaufgabe
1 Problemstellung
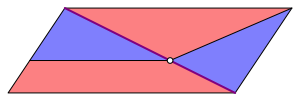
Abb. 1: Problemstellung
Auf einer der beiden Diagonalen eines Parallelogramms soll ein Teilpunkt so gefunden werden, dass das rote Trapez und das roten Dreieck flŠchengleich sind.
2 Bearbeitung
Da die Problemstellung affin invariant ist, kšnnen wir uns auf das Einheitsquadrat gemŠ§ der Abbildung 2 beschrŠnken.
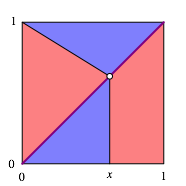
Abb. 2: Im Quadrat
Wenn die roten Figuren flŠchengleich sein sollen, mŸssen auch die beiden blauen Dreiecke flŠchengleich sein.
Das untere
blaue Dreieck ist rechtwinklig gleichschenklig mit der SchenkellŠnge x und hat den FlŠcheninhalt 
:
(1)
Das obere
blaue Dreieck hat die Grundlinie 1 und die dazugehšrige Hšhe 
. Sein FlŠcheninhalt 
ist daher:
(2)
Aus 
ergibt
sich die quadratische Gleichung:
(3)
Diese hat die positive Lšsung:
(4)
Dabei ist
(5)
der Goldene Schnitt (Walser 2013).
Die Diagonale muss also im VerhŠltnis des Goldenen Schnittes geteilt werden.
Die roten Figuren sind flŠchenmŠ§ig grš§er als die blauen. Das FlŠchenverhŠltnis ist ebenfalls der Goldene Schnitt.
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Weblink
Hans Walser: Goldene FŠchenaufteilung:
www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Flaechenaufteilung/Goldene_Flaechenaufteilung.htm