Hans Walser, [20170813]
Der Teufel sitzt im Detail
1 Worum geht es?
Erfahrungsgem§ sind Beweise des Satzes von Pythagoras ein sehr beliebtes Thema fr Semester- oder Diplomarbeiten bei Lehramtskandidaten der Sekundarstufe 1 (vgl. die schne Arbeit (Maresch und Promberger 2017)).
Bei meinen Studierenden ergaben sich dann immer wieder interessante Diskussionen ber die Stimmigkeit der von ihnen vorgestellten Beweise. Es ist eine didaktische Herausforderung, einen falschen Beweis fr einen an sich wahren Satz einsichtig zu machen. Dabei ist es nicht mglich, wie bei einem falschen Satz einfach mit einem Gegenbeispiel zu operieren. Vielmehr muss eine inkonsistente logische Struktur aufgezeigt werden.
Ich bin dabei oft mit fast trotzigen Antworten konfrontiert worden: Aber es stimmt doch! Die Stimmigkeit eines Satzes garantiert aber noch nicht die Richtigkeit des vorgelegten Beweises.
Im Folgenden werden einige falsche, fragwrdige oder schwindelerregende Beweise des Satzes von Pythagoras vorgestellt.
Es wird die bliche Notation fr das rechtwinklige Dreieck verwendet.
2 Der Klassiker
Der absolute Klassiker besteht darin, den Satz von Pythagoras als Sonderfall des Kosinus-Satzes zu sehen. Dabei wird bersehen, dass die in der Schule bliche Herleitung des Kosinus-Satzes den Satz von Pythagoras bentzt. Also wre es ein Zirkelschluss, damit den Satz von Pythagoras beweisen zu wollen.
Gleichwohl ist es sinnvoll, nach der Herleitung des Kosinus-Satzes auf den Sonderfall des rechtwinkligen Dreieckes hinzuweisen. Das ist einerseits ein cross check und andererseits eine Einbettung des neuen Satzes in schon vorhandenes Basiswissen.
Zum Nachdenken: Gibt es eine pythagorasfreie Herleitung des Kosinus-Satzes?
3 Trigonometrie
Aus
![]() (1)
(1)
folgt:
![]() (2)
(2)
Wegen der trigonometrischen Identitt
![]() (3)
(3)
folgt unmittelbar der Satz von Pythagoras.
Der Schwachpunkt liegt auf der Hand: die bombastische Formulierung ãtrigonometrische IdentittÒ darf nicht darber hinwegtuschen, dass zum Beweis von (3) in der Regel der Satz von Pythagoras verwendet wird.
4 Invariante
Mathematik ist das Auffinden von Invarianten. Fast jeder Satz der Mathematik kann mit einer Invarianten formuliert werden.
Der Satz von Pythagoras kann als Invariante interpretiert werden wie folgt (Abb. 1).
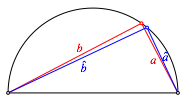
Abb. 1: Vernderung des Dreiecks
Wird die Ecke mit dem rechten Winkel auf dem Thaleskreis bewegt, bleibt die Summe der Kathetenquadrate invariant:
![]() (4)
(4)
Ist diese
Invarianz einmal nachgewiesen, ergibt sich durch den Grenzfall ![]() (oder
(oder ![]() ) die bliche Formulierung des Satzes von Pythagoras.
) die bliche Formulierung des Satzes von Pythagoras.
Allerdings knnen sich beim Invarianznachweis Fehler und Ungreimtheiten einschleichen.
4.1 Der schmutzige Trick von Newton
Bei einer kleinen Verschiebung der Ecke mit dem rechten Winkel auf dem Thaleskreis entsteht ein kleines Dreieck (Abb. 2, Lupe), das zum Ausgangsdreieck einigerma§en hnlich ist. Und zwar ist:
![]() (5)
(5)
Dies kann
mit einem kleinen ![]() in der
Form
in der
Form
![]() (6)
(6)
geschrieben werden.
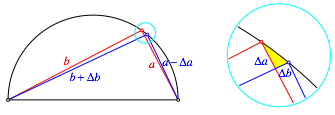
Abb. 2: Der schmutzige Trick von Newton
Daraus ergibt sich:
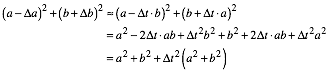 (7)
(7)
Der
schmutzige Trick von Newton (Ausdruck einer Studierenden) besteht nun darin, Quadrate
und hhere Potenzen eines kleinen Ausdrucks wegzulassen. Weglassen von ![]() ergibt aus
(7) die Pythagoras-Invarianz.
ergibt aus
(7) die Pythagoras-Invarianz.
Ist dieser Beweis in Ordnung?
4.2 Konstante Funktion
Wir
fassen (2) als Funktion von ![]() auf:
auf:
![]() (8)
(8)
Nun
leiten wir nach ![]() ab:
ab:
![]() (9)
(9)
Die Funktion ist eine Konstante. Wir erhalten also die Pythagoras-Invarianz.
Die Frage ist, ob in den Ableitungsregeln fr die Sinus- oder Kosinusfunktion nicht irgendwo versteckt schon der Satz von Pythagoras vorhanden ist.
Versuchen wir es ohne Ableiten mit einer Differenzbildung und den Additionstheoremen. Das gibt einiges an Rechnung:
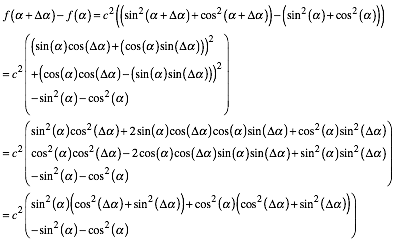 (10)
(10)
Wenn wir jetzt die trigonometrische Identitt (3) anwenden drften, wren wir ber dem Berg und erhielten die Invarianz:
![]() (11)
(11)
5 Didaktisches
In unserem Schulsystem durchluft jede Schlerin und jeder Schler verschiedene Schulstufen, Schulsysteme und Klassen mit verschiedenen Lehrpersonen. Das bringt mich sich, dass kaum einer Schlerin oder einem Schler ein logisch konsistenter lckenloser Aufbau der Mathematik dargereicht wird. Dies gilt insbesondere dann, wenn eine Schulstufe wie etwa die Sekundarstufe 1 mehrere Ziele (Vorbereitung fr Berufslehre und Vorbereitung aufs Gymnasium) zu erreichen hat.
Was im Unterricht als ãBeweisÒ bezeichnet wird, ist in aller Regel kein Beweis from first principles, sondern eine Verortung im schulischen Umfeld. Ob alle Stze in diesem Umfeld bewiesen sind, lsst sich nicht berprfen und ist auch unterschiedlich fr verschiedene Schlerinnen und Schler. Der Sinn dieser Beweise liegt dann auch nicht im Fixieren ewiger Wahrheiten, sondern im Erleben des lebendigen Geistes. Daher ist es gut und lehrreich, auch mit falschen Beweisen konfrontiert zu werden.
Literatur
Maresch, Gnter und Promberger, Janine (2017): Die mehr als 400 Beweise des Satzes von Pythagoras – eine mathematisch-geometrische Schatzkiste fr alle Schulstufen. IBDG, Informationsbltter der Geometrie (36), Heft 1/2017, 16-20.