Hans Walser, [20180604], [20180727]
Thaleskreis an Ellipse und Hyperbel
1 Ellipse
1.1 Thaleskreis
Die Menge der Punkte, von denen aus eine Ellipse unter einem rechten Winkel gesehen wird, ist ein Kreis (Abb. 1).
Bei einer Ellipse mit den Halbachsen a und b hat dieser Kreis den Radius r:
![]() (1)
(1)
Die Thaleskurve einer Ellipse ist also ein Kreis. Die Ecken der ãUmrechteckeÒ einer Ellipse liegen auf einem Kreis.
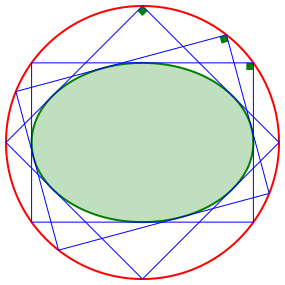
Abb. 1: Ellipse und Kreis
1.2 Sonderflle
a) Fr b = 0 wird die Ellipse zu einer Strecke und wir erhalten den gewhnlichen Thaleskreis.
b) Fr a = b ist die Ellipse ein Kreis (Abb. 2a). Der Thaleskreis ist trivial
(Abb. 2b). Er hat den Radius ![]() .
.
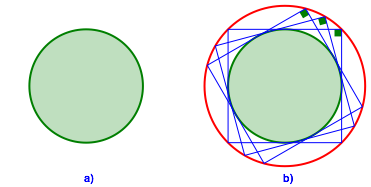
Abb. 2: Sonderfall des Kreises
1.3 Beweise
Wir zeigen zwei rechnerische Beweise
1.3.1 Beweis mit Parameterdarstellung
Fr die Ellipse verwenden wir die Parameterdarstellung:
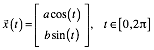 (2)
(2)
1.3.1.1 Tangenten
Die
Tangente mit Berhrpunktparameter ![]() hat die
Parameterdarstellung:
hat die
Parameterdarstellung:
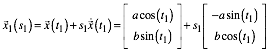 (3)
(3)
Entsprechend
die Tangente mit Berhrpunktparameter ![]() :
:
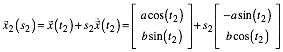 (4)
(4)
Fr den Schnittpunkt S erhalten wir die Koordinaten:
![]() (5)
(5)
1.3.1.2 Orthogonale Tangenten
Die Orthogonalittsbedingung ![]() fhrt auf:
fhrt auf:
![]() (6)
(6)
Daraus ergibt sich:
![]() (7)
(7)
Wir setzen dies in (5) ein und prfen, ob dann:
![]() (8)
(8)
Dies ist tatschlich der Fall (mit CAS nachgeprft).
Somit liegt der Schnittpunkt S auf dem Thaleskreis.
1.3.2 Erster Beweis mit quadratischen Gleichungen
Wir beginnen mit dem Punkt P auf dem Thaleskreis:
![]() (9)
(9)
Die x-Koordinate des Punktes P ist also ein freier Parameter. Der Punkt P liegt auf dem oberen Halbkreis, dies ist aus Symmetriegrnden aber keine Beschrnkung der Allgemeinheit.
Weiter hat die Ellipse die Gleichung:
![]() (10)
(10)
Wir nehmen das Geradenbschel durch P:
![]() (11)
(11)
Dabei ist m die Steigung der Bschelgeraden.
Wir
schneiden die Ellipse mit dem Geradenbschel, das hei§t wir lsen das aus (10)
und (11) bestehende quadratische Gleichungssystem nach ![]() auf.
auf.
Wir erhalten die beiden x-Werte:
 (12)
(12)
Fr eine berhrende Tangente sollten wir aber genau eine Lsung haben. Daher muss der Radikand in der gro§en Wurzel null sein. Dies ergibt eine quadratische Gleichung fr m:
![]() (13)
(13)
Wir erhalten die beiden Lsungen:
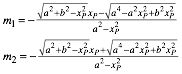 (14)
(14)
Dies sind die Steigungen der beiden Tangenten von P an die Ellipse. Wegen
![]() (15)
(15)
sind die beiden Tangenten orthogonal.
1.3.3 Zweiter Beweis mit quadratischen Gleichungen
Wir arbeiten mit der Ellipsengleichung:
![]() (16)
(16)
Der Punkt
P habe die Koordinaten
![]() .
.
Nun machen wir folgende Fallunterscheidung:
1.3.3.1 Senkrechte Tangente
Wenn ![]() ist haben
wir eine senkrechte Tangente, welche die Ellipse in einem der beiden spitzen
Scheitel berhrt. Eine dazu orthogonale Tangente berhrt in einem der beiden
stumpfen Scheitel, also ist
ist haben
wir eine senkrechte Tangente, welche die Ellipse in einem der beiden spitzen
Scheitel berhrt. Eine dazu orthogonale Tangente berhrt in einem der beiden
stumpfen Scheitel, also ist ![]() . Der Punkt P
erfllt die Bedingung:
. Der Punkt P
erfllt die Bedingung:
![]() (17)
(17)
Er liegt also auf dem Kreis mit dem Radius r gem§ (1).
1.3.3.2 Keine senkrechte Tangente
In diesem
Fall ist ![]() . Wir drfen also fr die Tangenten durch P mit dem Ansatz
. Wir drfen also fr die Tangenten durch P mit dem Ansatz
![]() (18)
(18)
arbeiten. Wir setzen (18) in (16) und erhalten die quadratische Gleichung fr x:
![]() (19)
(19)
Diese quadratische Gleichung (19) hat die beiden Lsungen:
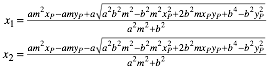 (20)
(20)
Fr eine Tangente bentigen wir eine Doppellsung. Es muss also die Diskriminante in (20) verschwinden:
![]() (21)
(21)
Dies ist eine quadratische Gleichung fr m. Sie hat die beiden Lsungen:
![]() (22)
(22)
Das sind die Steigungen der beiden von P ausgehenden Tangenten an die Ellipse. Die Orthogonalittsbedingung
![]() (23)
(23)
liefert nach einigen Rechnungen:
![]() (24)
(24)
Der Punkt P liegt also auf dem Kreis mit dem Radius r gem§ (1).
2 Hyperbel
2.1 Thalesfigur
Die Thalesfigur existiert nur fr ![]() und ist
ebenfalls ein Kreis. Dieser Thaleskreis hat den Radius r:
und ist
ebenfalls ein Kreis. Dieser Thaleskreis hat den Radius r:
![]() (25)
(25)
Fr ![]() liegen die
Hyperbelste im spitzwinkligen Bereich der Asymptoten (Abb. 3).
liegen die
Hyperbelste im spitzwinkligen Bereich der Asymptoten (Abb. 3).
Die Asymptoten zerlegen den Thaleskreis in zwei kleine Bgen im spitzwinkligen Bereich und zwei gro§e Bgen im stumpfwinkligen Bereich.

Abb. 3: Hyperbel und Thaleskreis
Die von Punkten auf einem kleinen Bogen des Thaleskreises ausgehenden Tangenten berhren beide denselben Hyperbelast. Dieser Hyperbelast liegt im Innern des Rechtwinkelbereiches der beiden Tangenten.
Die von Punkten auf einem gro§en Bogen des Thaleskreises ausgehenden Tangenten berhren beide Hyperbelste. Die beiden Hyperbelste liegen au§erhalb des Rechtwinkelbereiches der beiden Tangenten. Um die Hyperbel zu sehen, bruchte es eine Fischaugenkamera.
Fr die Punkte des Thaleskreises auf den Asymptoten haben wir einen interessanten Sonderfall (Abb. 4).
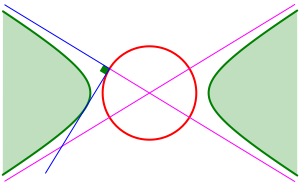
Abb. 4: Sonderfall auf den Asymptoten
Fr den
Sonderfall ![]() (gleichseitige Hyperbel) schrumpft der
Thaleskreis zu einem Punkt und die ãTangentenÒ sind die Asymptoten.
(gleichseitige Hyperbel) schrumpft der
Thaleskreis zu einem Punkt und die ãTangentenÒ sind die Asymptoten.
2.2 Beweise
2.2.1 Beweis mit Parameterdarstellung
Ein allgemeiner Beweis analog zur Ellipse ist mir nicht gelungen. Das Problem liegt darin, dass die Parameterdarstellung
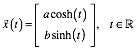 (26)
(26)
nur den rechten Hyperbelast liefert, wir aber beide Hyperbelste bentigen.
2.2.2 Erster Beweis mit quadratischen Gleichungen
Der Beweis geht analog zum entsprechenden Beweis bei der Ellipse. Es ndern lediglich einige Vorzeichen.
Wir beginnen mit dem Punkt P auf dem Thaleskreis (man beachte den genderten Radius des Thalekreises):
![]() (27)
(27)
Die x-Koordinate des Punktes P ist also ein freier Parameter. Der Punkt P liegt auf dem oberen Halbkreis, dies ist aus Symmetriegrnden aber keine Beschrnkung der Allgemeinheit.
Weiter hat die Hyperbel die Gleichung:
![]() (28)
(28)
Wir nehmen das Geradenbschel durch P:
![]() (29)
(29)
Dabei ist m die Steigung der Bschelgeraden.
Wir
schneiden die Hyperbel mit dem Geradenbschel, das hei§t wir lsen das aus (28)
und (29) bestehende quadratische Gleichungssystem nach ![]() auf.
auf.
Wir erhalten die beiden x-Werte:
 (30)
(30)
Fr eine berhrende Tangente sollten wir aber genau eine Lsung haben. Daher muss der Radikand in der gro§en Wurzel null sein. Dies ergibt eine quadratische Gleichung fr m:
![]() (31)
(31)
Wir erhalten die beiden Lsungen:
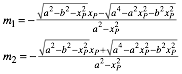 (32)
(32)
Dies sind die Steigungen der beiden Tangenten von P an die Hyperbel. Wegen
![]() (33)
(33)
sind die beiden Tangenten orthogonal.
2.2.3 Zweiter Beweis mit quadratischen Gleichungen
Der Beweis geht analog zum entsprechenden Beweis bei der Ellipse. Es ndern einige Vorzeichen.
Wir arbeiten mit der Hyperbelgleichung:
![]() (34)
(34)
Der Punkt
P habe die Koordinaten
![]() .
.
Der Fall ![]() ist nicht
mglich, weil es dazu keine orthogonale Tangente gibt. Es gibt also keine
Lsung mit einer senkrechten Tangente und wir drfen fr die Tangenten durch P mit dem Ansatz
ist nicht
mglich, weil es dazu keine orthogonale Tangente gibt. Es gibt also keine
Lsung mit einer senkrechten Tangente und wir drfen fr die Tangenten durch P mit dem Ansatz
![]() (35)
(35)
arbeiten. Wir setzen (35) in (34) und erhalten die quadratische Gleichung fr x:
![]() (36)
(36)
Diese quadratische Gleichung (36) hat die beiden Lsungen:
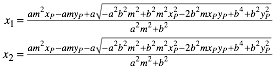 (37)
(37)
Fr eine Tangente bentigen wir eine Doppellsung. Es muss also die Diskriminante in (20) verschwinden:
![]() (38)
(38)
Dies ist eine quadratische Gleichung fr m. Sie hat die beiden Lsungen:
![]() (39)
(39)
Das sind die Steigungen der beiden von P ausgehenden Tangenten an die Ellipse. Die Orthogonalittsbedingung
![]() (40)
(40)
liefert nach einigen Rechnungen:
![]() (41)
(41)
Der Punkt P liegt also auf dem Kreis mit dem Radius r gem§ (25).
Websites
Hans Walser: Sehwinkel bei Kegelschnitten
www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkel_Kegelschnitte/Sehwinkel_Kegelschnitte.htm