1 Worum geht es?

Wir lernen in der Schule, dass die Menge aller Punkte C, von denen aus eine gegebene Strecke AB unter einem rechten Winkel gesehen wir, ein Kreis ist. Dies ist der so genannte Thaleskreis über der Strecke AB. Diese Strecke ist ein Durchmesser des Thaleskreises. Der Thaleskreis ist der Umkreis des rechtwinkligen Dreieckes ABC.

So ungefähr. Wie sieht das in der sphärischen und in der hyperbolischen Geometrie aus?

Wir werden sehen, dass der Begriff Thaleskreis nur in der euklidischen Geometrie sinnvoll ist.

2 Vorbereitungen

Der Weg nach Amerika geht über den Atlantik. Wir brauchen einige Vorbereitungen, um uns an das Thema machen zu können.

2.1 Konformität

Da ein rechter Winkel im Spiel ist, arbeiten wir in winkeltreuen (konformen) Modellen. Für die sphärische Geometrie ist dies das stereografische Bild, für die hyperbolische Geometrie das Kreismodell von Poincaré. Beide Modelle sind auch kreistreu. Aber was ist ein Kreis?

2.2 Kreise

Unter einem Kreis verstehen wir die Menge aller Punkte, die von einem festen Punkt (Mittelpunkt) einen konstanten Abstand (Radius) haben. In beiden Modellen ist das Bild eines Kreises wieder ein Kreis. Aber nun tritt eine Komplikation auf: Das Bild des Kreismittelpunktes ist nicht der Mittelpunkt des Bildkreises.

Am besten ein Beispiel.

Im Dreieck ABC in der hyperbolischen Geometrie sind die drei Mittelsenkrechten (Symmetrieachsen) , und der Seiten eingetragen, welche sich in einem Punkt U schneiden. Warum tun sie das eigentlich? Dieser Punkt U ist nun das Zentrum des hyperbolischen Umkreises u. Er ist aber offensichtlich nicht das planimetrische Kreiszentrum.

Die von U ausgehenden Kreisradien sind scheinbar ungleich lang. Das liegt daran, dass im Poincaré-Modell die Maßstäbe gegen den Rand zu verkürzt werden. In Wirklichkeit, das heißt in der hyperbolischen Geometrie, sind die von U ausgehenden Radien alle gleich lang.

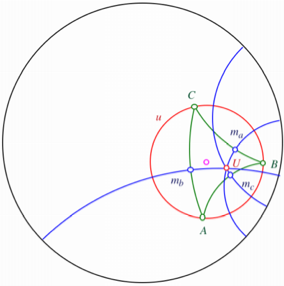
Umkreis

Nun wagen wir uns an die Analoga zum Thaleskreis.

3 Sphärische Geometrie

Vorerst ein Gedankenspiel: Auf der Kugel sei der Bogen AB ein Vierteilskreis, zum Beispiel in geografischen Koordinaten: und . Das ist die Hypotenuse des gesuchten rechtwinkligen Dreieckes. Nun suchen wir Punkte C, welche zu einem rechtwinkligen Dreieck ergänzen. Mögliche Lösungen sind natürlich die beiden Pole. Aber auch jeder Punkt auf dem Meridian zu 90°E ist eine Lösung, ebenso jeder Punkt auf dem 0°-Merdian. Die Thaleskurve ist also ein Zweieck, bestehend aus zwei Halbkreisen, welche sich orthogonal schneiden. (Wie ist es eigentlich mit der Verlängerung der Meridiane über die Pole hinaus?) Wenn wir nun die beiden Punkte A und B ein bisschen zusammen rücken lassen, ergibt sich aus Stetigkeitsgründen eine Figur, welche in der Nachbarschaft dieses Zweieckes verläuft. Das kann kein Kreis sein, daher die Terminologie Thaleskurve.

Im folgenden Beispiel ist der Äquator schwarz. Die Thaleskurve ist rot. Zusätzlich ist auch das diametrale Dreieck mit Thaleskurve eingezeichnet. Diametrale Figuren sind räumlich punktsymmetrisch, also kongruent, aber mit ungleichem Umlaufsinn.

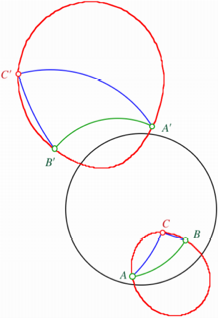
Rechtwinkliges Dreieck mit Thaleskurve

Die Thaleskurve ist offensichtlich kein Kreis, und insbesondere nicht der Umkreis des Dreieckes.

4 Hyperbolische Geometrie

Im folgenden Beispiel ist der Rand des Poincaré-Modells schwarz. Es ist ein rechtwinkliges Dreieck mit Thaleskurve eingezeichnet. Diese ist offensichtlich kein Kreis, insbesondere nicht der Umkreis.

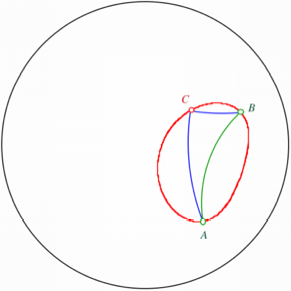
Rechtwinkliges Dreieck mit Thaleskurve

5 Die gute alte Leuchtturmaufgabe

Man lässt die Strahlen zweier Leuchttürme synchron, aber mit einer Phasenverschiebung drehen. Der Schnittpunkt der beiden Strahlen wandert auf einem Ortsbogen (in Deutschland Fasskreis genannt). Ist die Phasenverschiebung genau 90°, haben wir den Sonderfall des Thaleskreises.

5.1 Didaktische Kritik

Die Aufgabe ist schon vier Generationen alt. Zur Sicherung in der Seefahrt wurden nach den Leuchttürmen folgende Systeme verwendet: LORAN-C (Long Range Navigation), Radar (Radio Detection and Ranging), GPS (Gobal Positioning System).

Ist die Sache wenigstens mathematisch korrekt? Dazu drehen wir in zwei Punkten A und B je einen Großkreis beziehungsweise eine geodätische Linie (Analoga zu Geraden in der sphärischen und der hyperbolischen Geometrie) synchron, aber mit einer Phasenverschiebung. Der Aufgabe zuliebe verwenden wir die Phasenverschiebung 90°. Wie sieht die Ortslinie der Schnittpunkte aus?

5.2 Sphärische Geometrie

Die Leuchtturmaufgabe auf der Kugel

Wir sehen, dass es wiederum keinen Kreis ergibt. Und obwohl die Summe der Winkel bei A und B den Wert 90° ergibt, ist der Winkel bei C größer als 90°. Zudem ist dieser Winkel variabel. Wir erhalten also keine Thaleskurve.

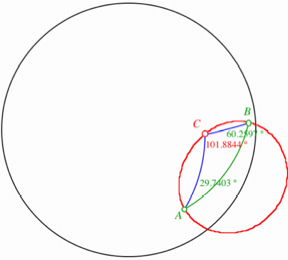
5.3 Hyperbolische Geometrie

Hier sind verschiedene Fälle möglich. In der Abbildung sehen wir die Ortskurve der Schnittpunkte, welche offensichtlich kein Kreis ist und sogar in zwei Teile zerfällt, und einen veritablen Schnittpunkt C. Obwohl die Summe der Winkel bei A und B den Wert 90° ergibt, ist der Winkel bei C kleiner als 90°. Zudem ist dieser Winkel variabel. Wir erhalten also keine Thaleskurve.

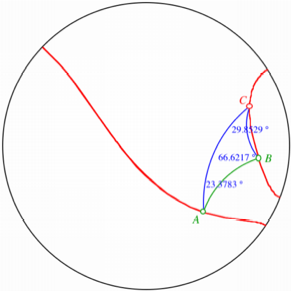
Leuchtturmaufgabe in der hyperbolischen Geometrie

Es ist aber durchaus möglich, dass die beiden von A und B ausgehenden Strahlen keinen Schnittpunkt haben. Die beiden Strahlen sind trotz Phasenverschiebung von 90° parallel.

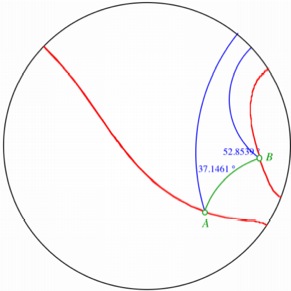
Kein Schnittpunkt

Zwischen diesen beiden Fällen gibt es einen Grenzfall. Die Strahlen schneiden sich auf dem Rand des Poincaré-Modells. Da dieser Rand aber nicht mehr zur hyperbolischen Ebene gehört, heißt das, dass sich die Strahlen nicht schneiden. Sie sind parallel. Man spricht in diesem Fall von Grenzparallelen.

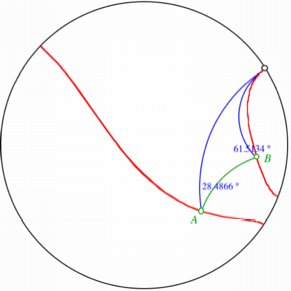
Grenzfall

Natürlich haben wir beim zweiten Teil der Ortskurve nochmals Grenzfälle und veritable Schnittpunkte.

6 Hintergrund

In der sphärischen wie in der hyperbolischen Geometrie sind die Winkelsumme in einem Dreieck nicht konstant. Der Überschuss (sphärischer Exzess) beziehungsweise das Manko (hyperbolisches Defizit) gegenüber 180° ist proportional zur Dreiecksfläche.

Die Konstanz der Winkelsumme im Dreieck in der Euklidischen Geometrie wird mit Sätzen an Parallelen bewiesen. In der sphärischen und der hyperbolischen Geometrie haben wir aber keine eindeutig bestimmte Parallele.

Der Begriff Thaleskreis ist nur in der euklidischen Geometrie sinnvoll. Dasselbe gilt für den Ortsbogen (in Deutschland Fasskreis genannt) und die zugehörigen Kreiswinkelsätze.

7 Technisches

Die Abbildungen wurden mithilfe von CAD (Cabri) erzeugt. Als Hilfsmittel empfehlen sich Makros zur Kreisspiegelung. Mit Cinerella geht es direkter.