Hans Walser, [20171009]

Thaleskurven

1 Worum geht es?

In einem beliebigen rechtwinkligen Dreieck mit der üblichen Beschriftung (Abb. 1) gilt auf Grund der Kathetensätze:

(1)

Daraus ergibt sich:

(2)

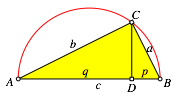
Abb. 1: Rechtwinkliges Dreieck

Wird der Thaleskreis abgeändert gemäß Abbildung 2, so gilt:

(3)

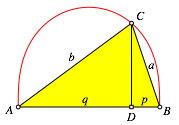
Abb. 2: Modifikation

Das Dreieck ist jetzt natürlich nicht mehr rechtwinklig.

Wie muss die rote Kurve in der Abbildung 2 beschaffen sein, damit für jedes C auf dieser Kurve die Beziehung (3) gilt?

Wie muss die Kurve beschaffen sein, damit für gegebenes k die Beziehung gilt:

(4)

2 Rechnerischer Beweis

Wir beweisen zunächst (2) rein rechnerisch. Dazu verwenden wir ein Koordinatensystem mit und . Der Thaleskreis ist dann der Graph der Funktion:

(5)

Der Punkt C habe die Koordinaten:

(6)

Weiter ist:

(7)

und:

(8)

Aus (7) und (8) folgt:

(9)

Damit ist (2) nachgewiesen.

3 Allgemeiner Fall

Es sei k gegeben.

Wir suchen eine Funktion , deren Graph als Kurve gemäß Abbildung 2 oder einer Verallgemeinerung davon dienen kann.

Es ist dann:

(10)

Weiter ist:

(11)

Weiter gilt nach wie vor (8). Die Bedingung (4) lautet demzufolge:

(12)

Wir können (12) nach auflösen und erhalten:

(13)

4 Bilder und Bemerkungen

Die folgenden Abbildungen zeigend die Kurven für verschiedene Werte von k.

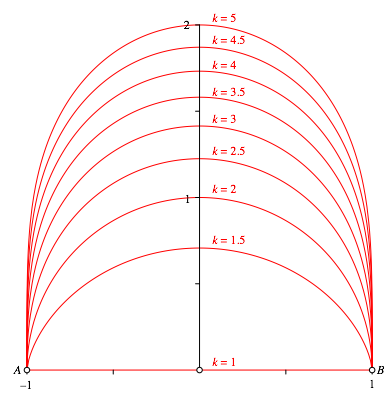
Abb. 3: Kurven

Für k = 1 ergibt sich die Strecke AB.

Für k = 2 ergibt sich der übliche Thaleskreis.

Für x = 0 ist (13) nicht definiert (Division durch null). Hingegen gilt (mit CAS validiert):

(14)

Die Kurven sind keine Ellipsen. In der Abbildung 4 ist rot die Kurve für k = 3 eingezeichnet und blau der mit dem Faktor gestreckte Thaleskreis, also die Ellipse.

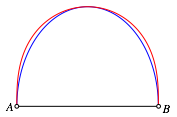
Abb. 4: Vergleich mit Ellipse