1 Worum es geht

Flächeninvarianz

2 Problemstellung

An die Seiten eines -Ecks setzen wir ähnliche gleichschenklige Trapeze an (Abb. 1 für ). Die Ecken werden durch komplexe Zahlen beschrieben, daher die Kleinschreibweise.

Abb. 1: Ähnliche gleichschenklige Trapeze

Die ähnlichen gleichschenkligen Trapeze haben die Ecken .

Nun zeichnen wir das -Eck ein (rot in Abb. 2).

Abb. 2: Rotes Vieleck

Analog zeichnen wir das -Eck ein (blau in Abb. 2).

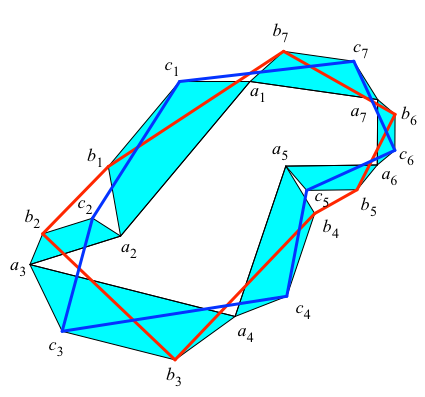
Abb. 3: Blaues Vieleck

Das rote und das blaue n-Eck haben denselben Flächeninhalt. Dies ist zu zeigen.

3 Bearbeitung

3.1 Formel

Ein durch komplexe Zahlen gegebenes -Eck hat den Flächeninhalt:

Da bei bedeuten der Realteil und die imaginäre Einheit. Diese Flächenformel ist eine Diskretisierung der Flächenformel von Stokes. Die Summe ist zyklisch zur verstehen, das heißt .

3.2 Rotes Vieleck

Es ist:

Dabei ist eine beliebige komplexe Zahl. Ihr Betrag gibt das Längenverhältnis der Schrägseiten der gleichschenkligen Trapeze zu den Basislinien an, ihr Argument ist der Anstellwinkel der Schrägseiten gegenüber der Basislinie.

Für die in der Flächenformel benötigte Summe erhalten wir:

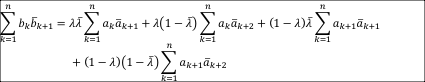
3.3 Blaues Vieleck

Es ist:

Für die in der Flächenformel benötigte Summe erhalten wir:

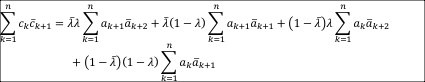
3.4 Vergleich

Beim Vergleich der beiden Summen sehen wir zunächst einige vermeintliche Unstimmigkeiten. Da unsere Summen aber zyklisch zu verstehen sind, ist:

Anschaulich: Wir steigen an einem anderen Punkt in die zyklische Summe ein.

Daher ist insbesondere:

Die beiden Flächenformeln ergeben also das gleiche Resultat für das rote wie das blaue Vieleck. Dies war zu zeigen.