Hans Walser, [20060812a]
Trigonometrie im Schachbrett
Anregung: H. S.
1 Ausgangslage
Die folgende Figur enthŠlt zwei rechtwinklige Dreiecke, das rote Dreieck ist das pythagoreische Dreieck mit den SeitenlŠngen 3, 4, 5. Die Figur lŠsst einen Zusammenhang zwischen den markierten Winkeln vermuten.
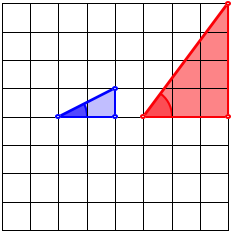
Winkel?
Es ist:
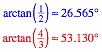
Wir vermuten:
![]()
2 Beweise
2.1 Rechnerischer Beweis
Zu zeigen ist:
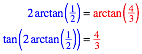
Unter Verwendung des Additionstheorems fźr den Tangens erhalten wir:
![]()
2.2 Beweis im Schachbrett
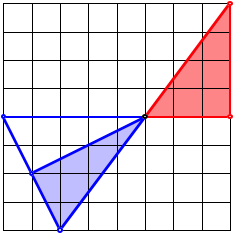
Beweis ohne Worte
3 Hintergrund
Die primitiven pythagoreischen Dreiecke kšnnen wie folgt parametrisiert werden:
Zu ![]() ,
, ![]() ,
, ![]() ,
, ![]() ist:
ist:
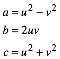
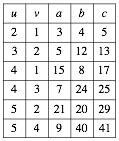
Beispiele:
In dieser Situation gilt:
![]()
Beweis rechnerisch:
![]()
Die folgende Figur
illustriert den Fall fźr ![]() mit
mit ![]() .
.
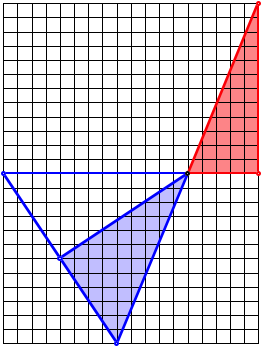
Beweis ohne Worte