Hans Walser, [20190907]

Türme

Anregung: P. M., G.

1 Worum geht es?

Kombinatorik. Zahlentheorie

2 Die Turm-Aufgabe

Eine Uraltaufgabe der Kombinatorik: auf wie viele Arten können acht paarweise feindliche Türme so auf einem Schachbrett aufgestellt werden, so dass keiner einen anderen schlagen kann?

Es muss in jeder Spalte und in jeder Zeile genau ein Turm stehen.

Die Abbildungen 1 und 2 zeigen je ein Beispiel. Worin besteht der Unterschied zwischen diesen beiden Beispielen?

Abb.1: Acht Türme

Abb. 2: Andere Anordnung

Die Türme der Abbildungen 1 und 2 besetzen zwar dieselben Felder im Schachbrett, sind aber intern anders angeordnet (die beiden Türme in den ersten beiden Spalten sind vertauscht).

Es gibt daher Möglichkeiten, nämlich 8! für die Auswahl der Felder und anschließend 8! für die Besetzung einer bestimmten Felderkonfiguration mit den einzelnen Türmen.

3 Nummerierung

Wir nummerieren die Felder des Schachbrettes von 0 bis 63 gemäß Abbildung 3.

Abb. 3: Nummerierung

Weiter markieren wir die Felder gemäß den Positionen der Türme der Abbildungen 1 und 2 (Abb. 4). Es gibt 8! = 40320 Markierungsmöglichkeiten.

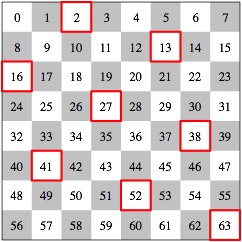
Abb. 4: Positionen der Türme

Die Summe der markierten Zahlen ist 252.

4 Anderes Beispiel

Die Abbildung 5 zeigt eine andere Positionsbelegung der Türme, die Abbildung 6 die zugehörigen Markierungen im nummerierten Schachbrett.

Abb. 5: Andere Positionsbelegung

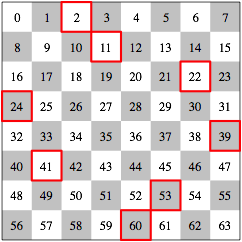
Abb. 6: Markierungen

Die Summe der markierten Zahlen ist wiederum 252.

5 Lehrer Lämpel

a) Gibt es bei allen 40320 Markierungsmöglichkeiten die Summe 252?

b) Warum ist das so?

c) Was ändert sich, wenn wir die Felder von 1 bis 64 nummerieren?

d) Wie ist es allgemein mit n Türmen in einem n×n-Schachbrett?

e) Warum sind die Summen immer durch 3 teilbar?

6 Bearbeitung der Fragen

Wir nummerieren die Felder mit dem Positionssystem auf der Basis 8 (Abb. 7).

Abb. 7: Positionssystem auf der Basis 8

In jeder Spalte haben wir jetzt immer dieselbe Einerziffer, und zwar der Reihe nach die Ziffern 0, 1, ... , 7. In jeder Zeile haben wir dieselbe Achterziffer, und zwar der Reihe nach die Ziffern 0, 1, ... , 7.

In der Abbildung 8 sind zusätzlich die Markierungen eingetragen, welche den Turmpositionen der Abbildungen 1, 2 und 4 entsprechen.

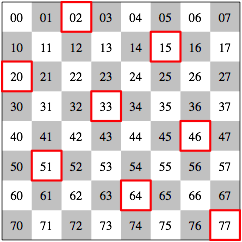
Abb. 8: Markierungen

Wir haben in jeder Spalte und in jeder Zeile genau einen Turm. Daher kommen in den markierten Feldern insgesamt genau die Einerziffern 0, 1, ... , 7 und ebenso die Achterziffern 0, 1, ... , 7 vor. Für die Gesamtsumme S heißt das:

(1)

Wenn wir von 1 bis 64 nummerieren, wird jede Zahl um 1 erhöht. Die Summe erhöht sich daher um 8. Wir erhalten die Summe 260.

In einem n×n-Schachbrett gilt entsprechend bei der Nummerierung von 0 bis :

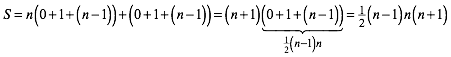
(2)

Da die Summe S bis auf den Faktor das Produkt dreier aufeinanderfolgender natürlicher Zahlen ist, ist sie durch 3 teilbar.

Der Quotient ist offenbar der Binomialkoeffizient .

Die Tabelle 1 zeigt die ersten Werte.

n	S
0	0	0	0
1	0	0	0
2	3	1	1
3	12	4	4
4	30	10	10
5	60	20	20
6	105	35	35
7	168	56	56
8	252	84	84
9	360	120	120
10	495	165	165

Tab. 1: Werte

Damit sind die Fragen des Lehrers Lämpel beantwortet. Das mit den Binomialkoeffizienten hat er offenbar nicht gewusst.