Hans Walser, [20160219]

Turm zu Papyron

1 Der Stapel

Wir zerlegen ein DIN-A4-Blatt in zwei DIN-A5-Blätter. Eines der beiden DIN-A5-Blätter zerlegen wir weiter in zwei DIN-A6-Blätter.

Nun legen wir eines der beiden DIN-A6-Blätter mittig auf das noch vorhandene DIN-A5-Blatt.

Das zweite DIN-A6-Blatt zerlegen wir ein zwei DIN-A7-Blätter und legen eines davon mittig auf das noch vorhandene DIN-A6-Blatt.

Und so weiter. Es entsteht ein Stapel.

2 Fragen

Frage 1: Ist dieser Stapel als „Pyramide“ oder als „Turm“ zu bezeichnen?

Frage 2: Wie hoch wird der Stapel?

3 Bearbeitung der Fragen

Die Abbildung 1 zeigt den Stapel von oben.

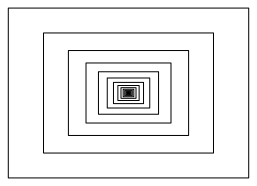
Abb. 1: Stapel aus der Sicht von oben

Aus dieser Sicht lässt sich nicht entscheiden, ob wir es mit einer Pyramide oder einem Turm zu tun haben (Frage 1).

Die Abbildung 2 zeigt den Stapel von vorne. Die Papierdicke ist konstant, da ja alle Lagen aus demselben Papierblatt geschnitten sind.

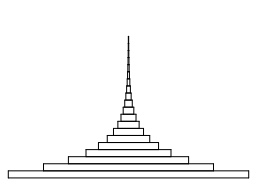
Abb. 2: Sicht von vorne

Der Stapel ist als „Turm“ zu bezeichnen. Der Turm kann beliebig hoch werden. Die Seitenkonturen des Stapels sind um 90° gedrehte Exponentialkurven.

Bei einer Pyramide dürften die Seitenkonturen nicht gekrümmt sein. Dies wäre dann der Fall, wenn die Papierdicke abnehmen würde (Abb. 3). Das ist aber nicht möglich, da alle Teile aus demselben Papierblatt geschnitten sind.

Abb. 3: Pyramide

Die Pyramide hätte – mit der Papierdicke d für die unterste Lage – die Gesamthöhe h:

(1)