Hans Walser, [20130120]

†bergangsmatrix

Anregung: B. J., B.

1     WechselwŠhler

In Yellowland gibt es nur zwei politische Parteien, die Schwarzen und die Roten. Die WŠhler bleiben in der Regel ihrer Partei treu. Allerdings wechseln bei jeder Wahl 20% der bisherigen Schwarz-WŠhler zu Rot, wŠhrend 10% der Rot-WŠhler zu Schwarz wechseln.

Bei den letzten Wahlen erhielten die Schwarzen 95% der Stimmen und bildeten daher die Regierung.

Wie sieht die politische Zukunft von Yellowland aus?

1.1    Prognosen sind schwierig

AnteilmŠ§ig wechseln mehr Schwarz-WŠhler zu rot als umgekehrt. Der Stimmenanteil der Schwarzen wird daher abnehmen, jedenfalls so lange Schwarz eine solide Mehrheit hat. Die Frage ist, ob Rot je eine Mehrheit erreichen kann.

1.2    Tabelle

Mit Excel ergibt sich:

Wahlperiode

Anteil Schwarz

Anteil Rot

0

0.950000

0.050000

1

0.765000

0.235000

2

0.635500

0.364500

3

0.544850

0.455150

4

0.481395

0.518605

5

0.436977

0.563024

6

0.405884

0.594116

7

0.384118

0.615882

8

0.368883

0.631117

9

0.358218

0.641782

10

0.350753

0.649247

11

0.345527

0.654473

12

0.341869

0.658131

13

0.339308

0.660692

14

0.337516

0.662484

15

0.336261

0.663739

16

0.335383

0.664617

17

0.334768

0.665232

18

0.334338

0.665662

19

0.334036

0.665964

20

0.333825

0.666175

Bereits nach vier weiteren WahlgŠngen hat Rot eine Mehrheit. So schnell kann das wechseln.

Auf Grund der Zahlen vermuten wir, dass sich schlie§lich eine stabile -Mehrheit fŸr Rot ergibt.

Die Abbildung zeigt die Datenpunkte.

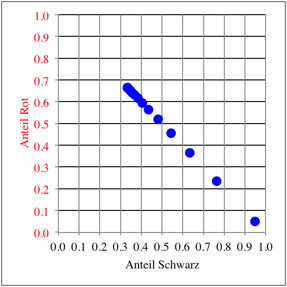
Datenpunkte

Da die Summe der gepaarten Daten immer 1 ist, liegen die Punkte auf der Geraden .

1.3    †bergangsmatrix

Wir fassen die Anteile von Schwarz und Rot zu einem Vektor zusammen und indizieren gemŠ§ der Wahlnummerierung, also in unserem Beispiel:

 

 

Damit gilt folgende Rekursion:

 

 

Die Matrix

 

 

hei§t †bergangsmatrix. Manchmal spricht man auch von einer Prozessmatrix oder stochastischen Matrix. Die Spaltensummen der †bergangsmatrix sind 1. Es hat keine negativen MatrixeintrŠge.

1.4    Eigenwerte und Eigenvektoren

FŸr die Matrix A finden wir die Eigenwerte und Eigenvektoren:

 

 

Beim Handrechnen ist man angenehm Ÿberrascht, wie schlank das geht. Liegt da ein prŠpariertes ãLehrerbeispielÒ vor?

Weiter ist der Eigenwert  Ÿberraschend, der zugehšrige Eigenvektor kann in der Form

 

 

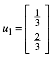
geschrieben werden und gibt die vermutete Grenzlage der Stimmenverteilung wieder. Wir vermuten also:

 

 

Der zweite Eigenvektor kann nicht so justiert werden, dass eine Spaltensumme 1 ergibt.

1.5    Beweis

Wir mšchten zeigen:

 

 

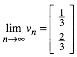
FŸr den Beweis schreiben wir  in der Form:

 

 

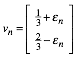
Diese Schreibweise ist immer mšglich, da die Vektoren die Spaltensumme 1 haben. Damit erhalten wir:

 

 

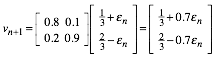
Somit ist , der ãFehlerÒ ist eine geometrische Nullfolge.

Der Faktor 0.7 ist sowohl die Determinante wie auch der zweite Eigenwert der Matrix. Ist das Zufall?

2     Allgemein

Wir studieren die †bergangsmatrix:

 

 

Dabei sei  und . (Die GrenzfŠlle werden unten separat diskutiert.)

Die Matrix A hat die Determinante . Es ist .

2.1    Eigenwerte und Eigenvektoren

Charakteristische Gleichung fŸr die Eigenwerte:

 

 

Diskriminante der quadratischen Gleichung:

 

 

Eigenwerte:

 

 

Der Eigenwert  in unserem Beispiel war also kein ãLehrerbeispielÒ, sondern liegt in der Natur der Sache. Den zugehšrigen Eigenvektor normieren wir auf die Spaltensumme 1 und erhalten:

 

 

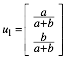
Der Eigenwert  ist die Determinante der Matrix A. Wir erhalten den zugehšrigen Eigenvektor:

 

 

Auch das ist ein alter Bekannter.

2.2    Folge und Grenzwert

Wir starten eine Folge  mit dem Startvektor

 

 

und der Rekursion:

 

 

Dann ist:

 

 

Beweis:

Da die †bergangsmatrix A und der Startvektor  die Spaltensumme 1 haben, ist dies fŸr alle Vektoren  der Fall.

Ein beliebiger Vektor der Folge kann daher in der Form

 

 

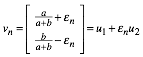
geschrieben werden. Wir setzen dies in die Rekursion ein:

 

 

Somit ist . Wegen  ist die Folge  eine Nullfolge. Damit ist die Behauptung bewiesen.

2.3    SonderfŠlle

Wir haben folgende Falltabelle:

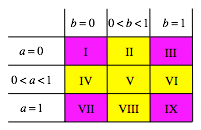
Falltabelle

Die gelb markierten FŠlle II, IV, V, VI, VIII sind regulŠr.

Im Fall I haben wir die Matrix A die Einheitsmatrix. Wir erhalten eine konstante Folge, welche durch den Startvektor gegeben ist.

Im Fall III haben wir die Matrix:

 

 

Zu beliebigem Startvektor ergibt sich nach einem Schritt die konstante Folge:

 

 

Im Fall VI haben wir die Matrix:

 

 

Zu beliebigem Startvektor ergibt sich nach einem Schritt die konstante Folge:

 

 

Im Fall IX schlie§lich ergibt sich die Matrix:

 

 

Mit dem Startvektor

 

 

erhalten wir zunŠchst

 

 

und weiter die alternierende Folge:

 

 

Es gibt keinen Limes.