Hans Walser, [20220809]

Ulam-Spirale

1 Worum geht es?

Grafische Spielerei im Kontext der Ulam-Spirale. Mustererkennung.

Explorative Studie

2 Die Ulam-Zahlenspirale

In einem Quadratmuster werden die Zahlen 0, 1, 2, ... spiralförmig eingetragen (Abb. 1) (Walser 2022, S. 97).

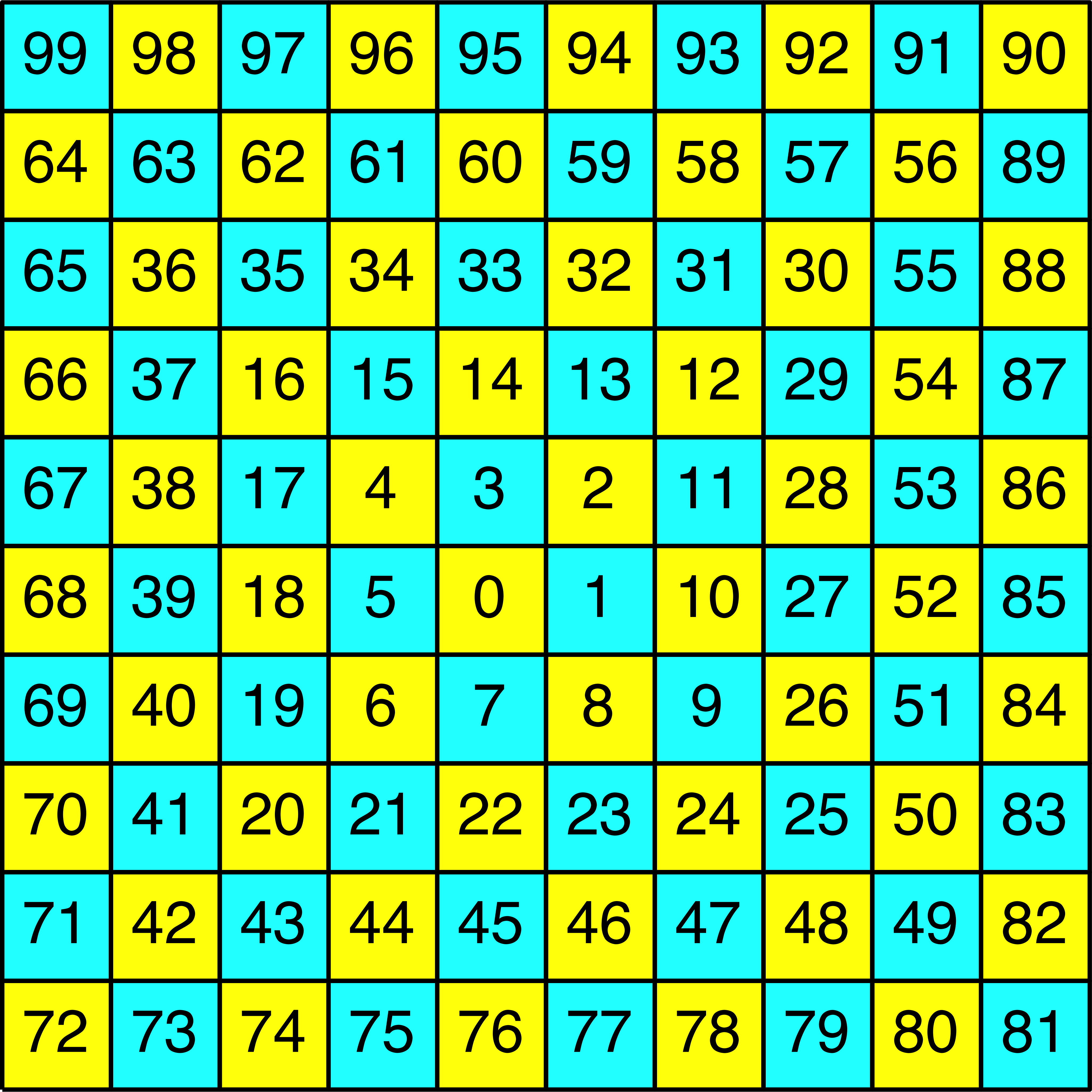
Abb. 1: Ulam-Zahlenspirale

3 Viertelkreise

In ein Quadratfeld zeichnen wir zwei gegenüberliegende Viertelkreise (Abb. 2). Die Viertelkreise haben die Zentren in gegenüberliegenden Quadratecken (links unten und rechts oben) und die halbe Quadratseite als Radius.

Abb. 2: Viertelkreise

4 Kombination

Wir passen in die Quadrate der Abbildung 1 solche Viertelkreise ein (Abb. 3). Es erschein ein wellenartiges Muster. Die Wellen laufen von links oben nach rechts unten.

Abb. 3: Viertelkreise einpassen

5 Verdrehungen

Wir können ein Quadratfeld mitsamt den beiden Viertelkreisen um 90° drehen. Der Anschluss an die Nachbarfelder bleibt bestehen.

In der Abbildung 4 wurden die Felder mit den Nummern 12 und 17 verdreht.

Abb. 4: Nummern 12 und 17 verdreht

6 Ulam

Stansiław Martin Ulam (1909-1984) entdeckte 1963, dass sich in der nach ihm benannten Zahlenspirale auffallend viele Primzahlen in diagonalen Linien befinden. Wir verdrehen daher in der Abbildung 3 sämtliche Quadratfelder mit einer Primzahl als Nummer (Abb. 5). Da 2 die einzige gerade Primzahl ist, erhalten wir dort eine grafische Besonderheit.

Abb. 5: Primzahlfelder verdreht

Die Abbildung 6 zeigt einen größeren Ausschnitt, aber ohne die Zahlen.

Abb. 6: Größerer Ausschnitt

7 Andere Verdrehungen

7.1 Zahlenmuster

Wir können die Quadratfelder nach anderen Kriterien verdrehen.

In der Abbildung7 sind alle Quadratfelder mit geraden Nummern verdreht.

Abb. 7: Gerade Zahlen verdreht

In der Abbildung 8 sind alle Quadratfelder verdreht, deren Nummern ein Vielfaches von drei sind.

Abb. 8: Dreierzahlen

Die Abbildung 9 illustriert die Viererzahlen.

Abb. 9: Viererzahlen

Die Abbildung 10 illustriert die Vielfachen von 5 bis 8.

Abb. 10.5: Fünferzahlen

Abb. 10.6: Sechserzahlen

Abb. 10.7: Siebnerzahlen

Abb. 10.8: Achterzahlen

Die Abbildungen 11 und 12 illustrieren die Quadratzahlen.

Abb. 11: Quadratzahlen. Versetzte Diagonale

Abb. 12: Quadratzahlen

In der Abbildung 13 sind die Zahlen relevant, welche als Produkt zweier aufeinanderfolgender natürlicher Zahlen geschrieben werden können. Beispiele: 12 = 3•4, 42 = 6•7.

Abb. 13: Andere Diagonale

7.2 Münzenwurf

In den Abbildungen 14 und 15 wird bei jedem Quadratfeld zufällig entschieden, ob es verdreht wird oder nicht.

Abb. 14: Kopf oder Zahl?

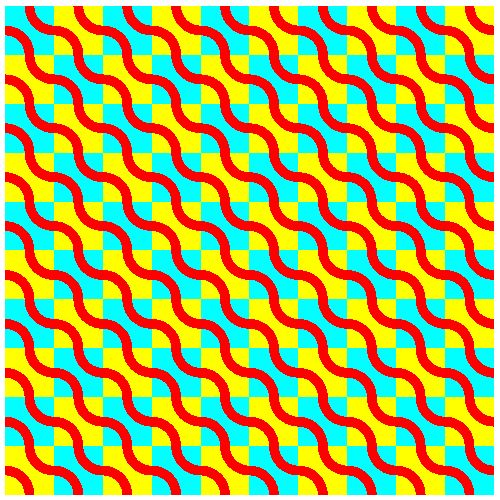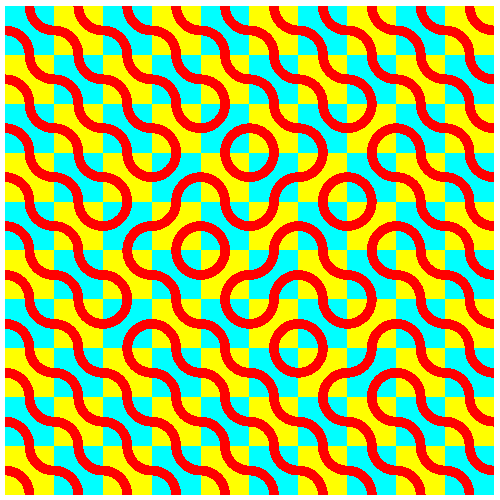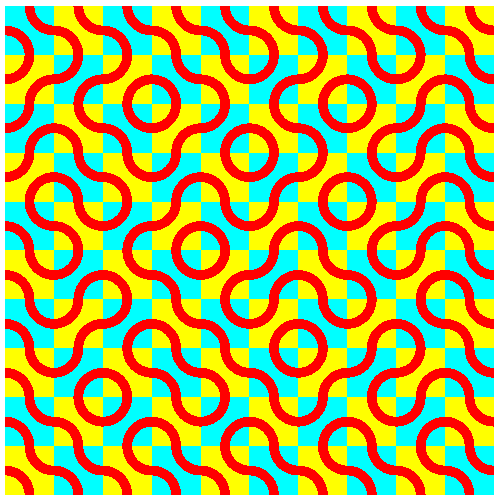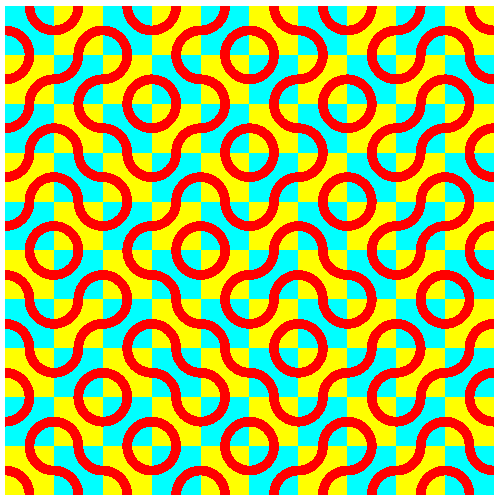
Abb. 15: Kopf oder Zahl?

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).

Weblinks

Hans Walser: Schachbrett

http://www.walser-h-m.ch/hans/Miniaturen/S/Schachbrett2/Schachbrett2.html

Hans Walser: Ulam-Zahlenspirale

http://www.walser-h-m.ch/hans/Miniaturen/U/Ulam/Ulam.html