Hans Walser, [20210802]

Ulam-Zahlenspirale

0 Worum geht es?

Zwei und dreidimensionale Beispiele der Ulam-Spirale

Explorative Studie

Bilder und Muster

1 Die Zahlenspirale

Die Abbildung 1 zeigt den Anfang einer eckigen Zahlenspirale.

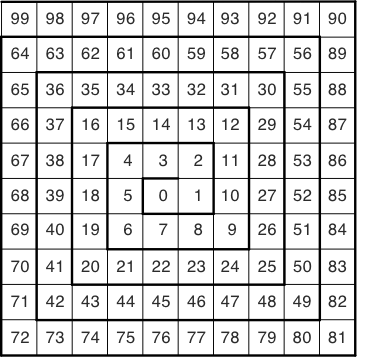
Abb. 1: Eckige Zahlenspirale

Die Anordnung der Zahlen in dieser Spirale enthält einige auffallende Eigenschaften. In den Ecken links oben und rechts unten sehen wir die Quadratzahlen (Abb. 2). Nach links oben die Quadrate der geraden, nach rechts unten die Quadrate der ungeraden Zahlen.

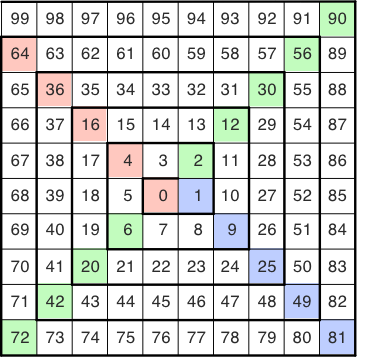
Abb. 2: Zahlen in den Ecken

Die Zahlen rechts oben und links unten sind jeweils die geometrischen Mittel der benachbarten Quadratzahlen. Beispiel: . Die Zahlen haben die Form . Beispiel: . Weiter gilt für die Zahlen in der grün markierten Diagonalen das Muster der Abbildung 3a. Die zweiten Differenzen sind konstant. Wir haben es mit einer sogenannten arithmetischen Folge zweiter Ordnung zu tun.

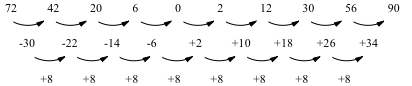
Abb. 3a: Die zweiten Differenzen sind konstant

Das Profil dieser Zahlen liegt daher auf einer nach oben offenen Parabel (Abb. 3b).

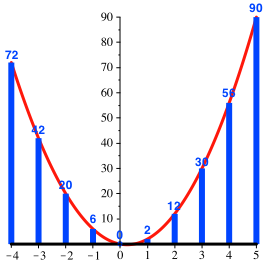
Abb. 3b: Profil der Zahlen

Eine bei 0 oder 1 beginnende nach außen verlaufende waagerechte, senkrechte oder schräge Zahlenfolge ist ebenfalls eine arithmetische Folge zweiter Ordnung. Die konstante Differenz ist 8.

2 Primzahlen

In der Abbildung 4 sind die Primzahlen markiert.

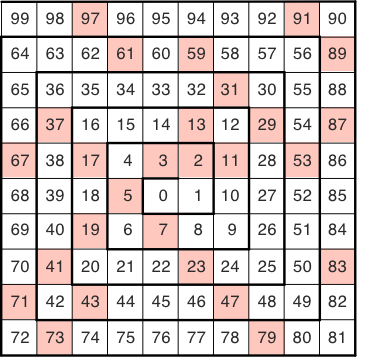
Abb. 4: Position der Primzahlen

Erstaunlich viele Primzahlen finden sich auf diagonalen Geraden. Diese Eigenschaft wurde 1963 von Stanisław Marcin Ulam (1909-1984) entdeckt. Die Spirale wird daher als Ulam-Spirale bezeichnet. Dabei ist die Startzahl in der Regel nicht 0, sondern 1. Das Rätsel dieser Primzahl-Positionierung ist bis heute nicht gelöst.

Die Abbildung 5 zeigt dasselbe, aber ohne Zahlen.

Abb. 5: Primzahlen rot

In der Abbildung 6 sind die Primzahlen zwischen 0 und 9999 angegeben. Wir sehen einige diagonale Muster.

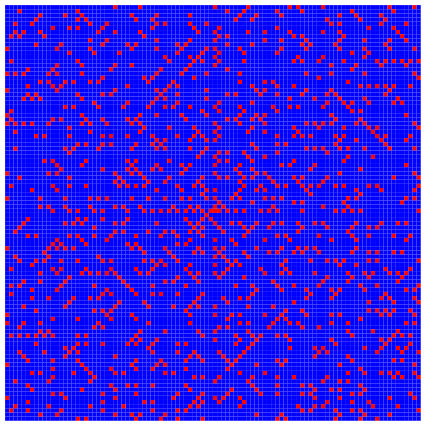
Abb. 6: Primzahlen rot

3 Modulo

3.1 Ungerade und gerade

Die ungeraden beziehungsweise geraden Zahlen sind nach einem Schachbrettmuster verteilt (Abb. 7).

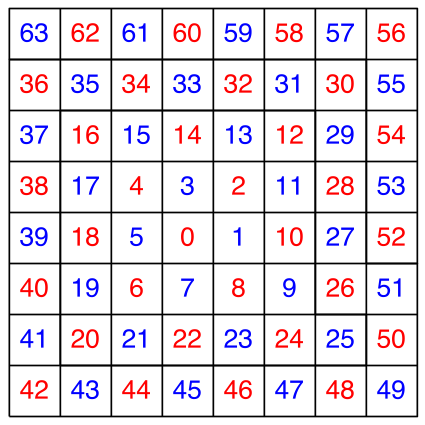
Abb. 7: Schachbrettmuster

Die roten Zahlen sind die „Zweierzahlen“.

In der Abbildungen 8 sind die Positionen der Vielfachen von 1, 2, 3, ... jeweils rot gefärbt.

Abb. 8.1: Modulo 1

Abb. 8.2: Modulo 2

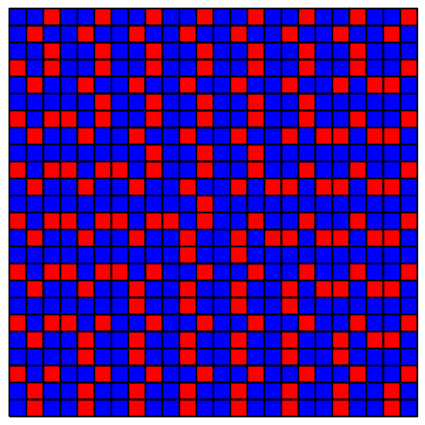
Abb. 8.3: Modulo 3

Abb. 8.4: Modulo 4

Abb. 8.5: Modulo 5

Abb. 8.6: Modulo 6

Abb. 8.7: Modulo 7

Abb. 8.8: Modulo 8

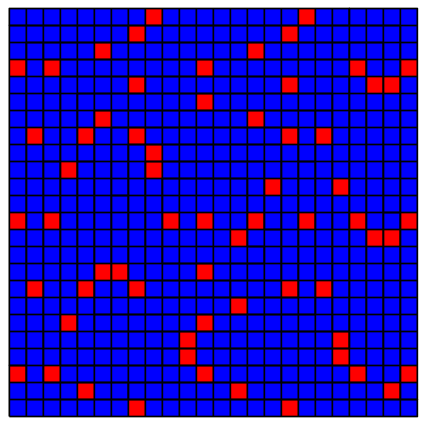
Abb. 8.9: Modulo 9

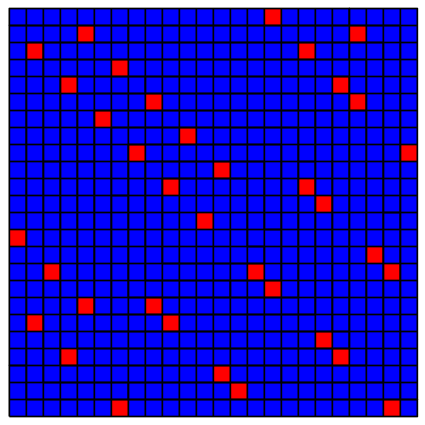
Abb. 8.16: Modulo 16

4 Farbspiralen

4.1 Spektrum auf ganze Spirale verteilt

Die Regenbogenfarben werden auf die gesamte vorhandene Spirale verteilt. Die Dezimalstelle der Abbildungsnummer gibt die Kantenlänge des Quadrates.

Abb. 9.2

Abb. 9.4

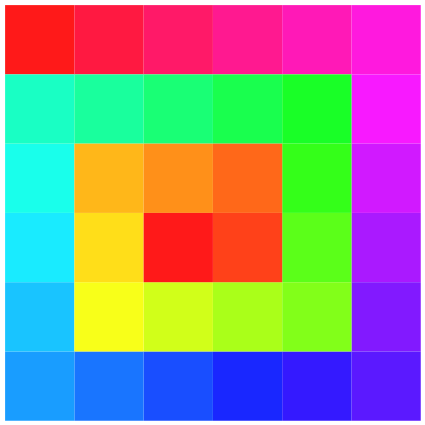
Abb. 9.6

Abb. 9.8

Abb. 9.16

Abb. 9.32

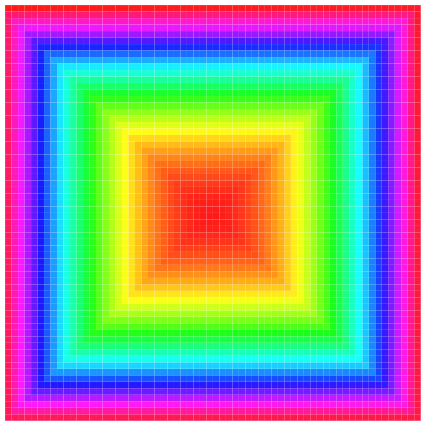
Abb. 9.64

Abb. 9.128

4.2 Spektrum auf Modullänge verteilt

Die Dezimalzahl der Abbildungsnummer gibt die Modullänge. Die Kantenlänge des Quadrates ist 24.

Abb. 10.1

Abb. 10.2

Abb. 10.3

Abb. 10.4

Abb. 10.5

Abb. 10.6

Abb. 10.7

Abb. 10.8

Abb. 10.9

Abb. 10.15

Abb. 10.16

Abb. 10.17

Abb. 10.31

Abb. 10.32

Abb. 10.33

Im folgenden Bild mit der Periodenlänge 32 ist die Kantenlänge 100.

Abb. 11: Modulzahl 32. Kantenlänge 100

5 Ulam-Türme

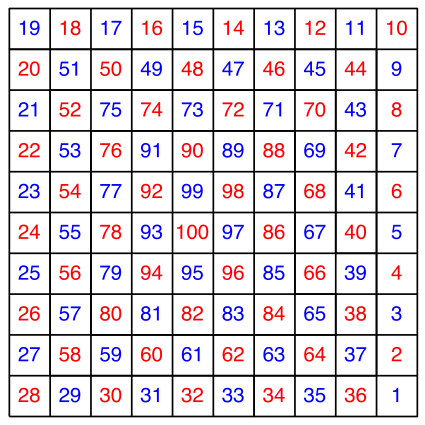
Abb. 12: Umkehrung der Reihenfolge

Wir ergänzen die Zahlen der Abbildung 1 auf 100 (Abb. 12). Damit wird die Reihenfolge umgekehrt. Die großen Zahlen sind in der Mitte. Es wird auch noch so gespiegelt, dass die Spirale mit zunehmenden Zahlen im positiven Drehsinn umläuft.

Das Profil dieser Zahlen ist nun eine nach unten offene Parabel.

Ein Histogramm zu dieser Zahlenspirale ist ein Turm.

Analog können wir auch mit kleineren Zahlenspiralen vorgehen. Die Turmhöhe ist das Quadrat der Seitenlänge des Bodenquadrates.

Die Abbildung 13 zeigt der Reihe nach die Türme für die Bodenkantenlängen 2, 4, 6, 8, 10 und 16.

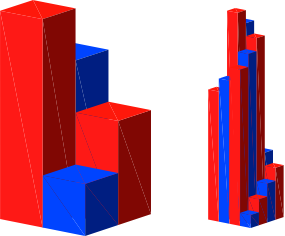
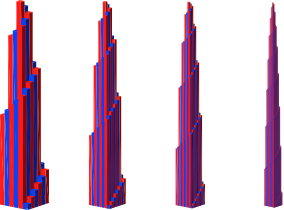
Abb. 13: Ulam-Türme

Die Abbildung 14 gibt dieselben Türme in der Regenbogenfärbung. Die Türme habeneine schwindelerregende Außentreppe mit einem Steigungswinkel 45°.

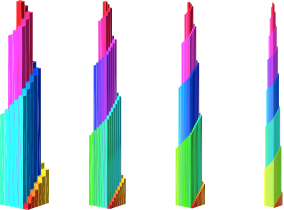
Abb. 14: Regenbogenfärbung

Die Abbildung 15 zeigt die ersten fünf Türme der Abbildung 14 in gleicher Skalierung. Wir sehen das quadratische Wachstum.

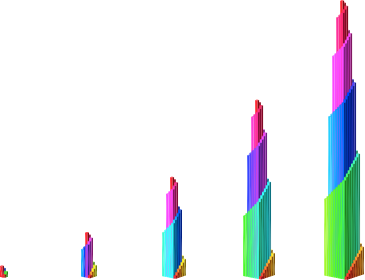
Abb. 15: Gleiche Skalierung

6 Unterhöhte Darstellung

Wir unterhöhen die Türme so, dass sie in einen Würfel hineinpassen. Die Abbildung 16 zeigt den unterhöhten Turm mit der Bodenkantenlänge 16. Die Treppen steigen sehr gemächlich an.

Das Profil des Turmes ist eine nach unten offene Parabel.

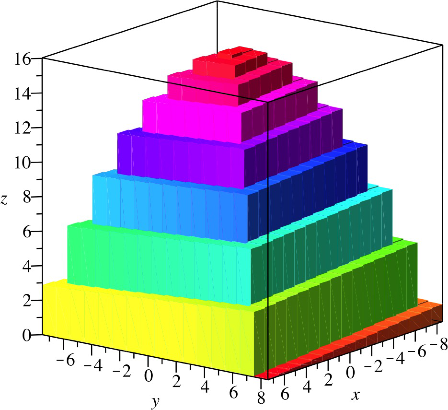
Abb. 16: Unterhöhte Darstellung

Die Abbildung 17 zeigt verschiedene Färbungen zur Bodenkantenlänge 50. Wir sehen auch deutlich das Parabelprofil.

Abb. 17.1: Paritätische Färbung

Abb. 17.2: Färbung modulo 3

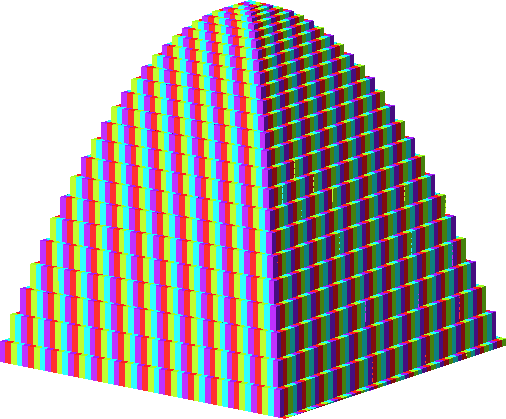
Abb. 17.3: Färbung modulo 4

Abb. 17.4: Färbung modulo 8

Abb. 17.5: Färbung modulo 64

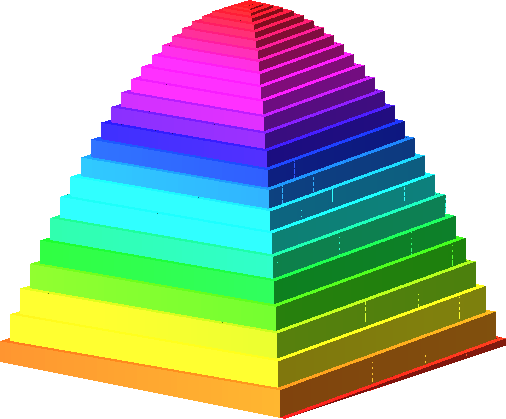
Abb. 17.6: Regenbogenfarben

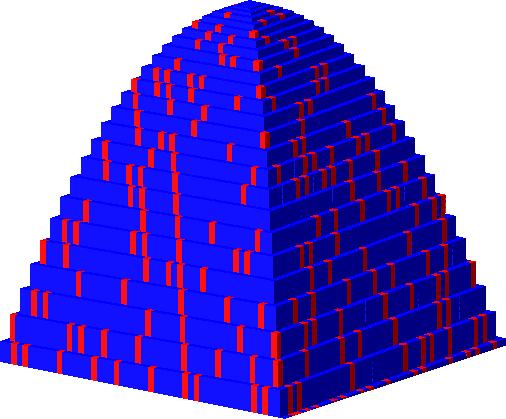
Abb. 17.7: Primzahlfärbung

7 Animation

Abb. 18: Färbung modulo 8

8 Quadratzahlen

Wir ersetzen die Zahlen in der Abbildung 12 durch deren Quadratzahlen (Abb. 19).

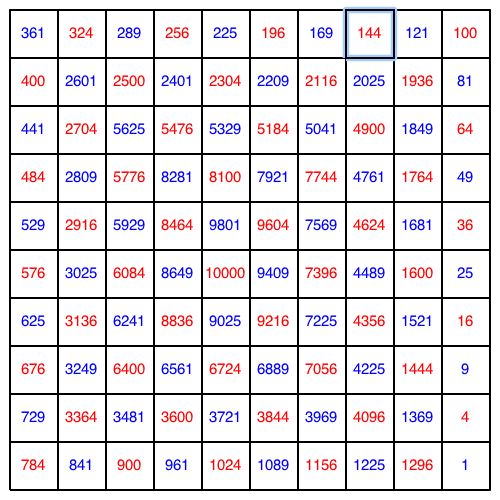
Abb. 19: Quadratzahlen

Die Abbildung 20 zeigt das Histogramm (unterhöht) auf der Basis der Quadratzahlen (Bodenkantenlänge 100, Farbmodul 64). Das glockenförmige Verhalten der Konturlinie verstehe ich nicht.

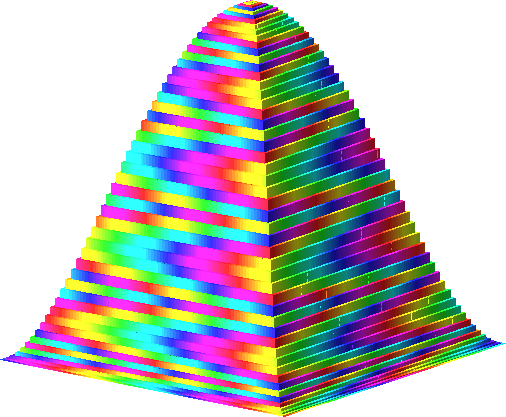
Abb. 20: Merkwürdige Figur

9 Ulam-Pyramide

Wir ersetzen die Zahlen der Abbildung 12 durch den Wert:

(1)

Dabei ist n die Laufnummer und N die größte Zahl. In der Abbildung 12 ist N = 100. Die Werte gemäß (1) sind in der Regel nicht ganzzahlig. In der Abbildung 21 sind diese Werte auf zwei Dezimalstellen gerundet.

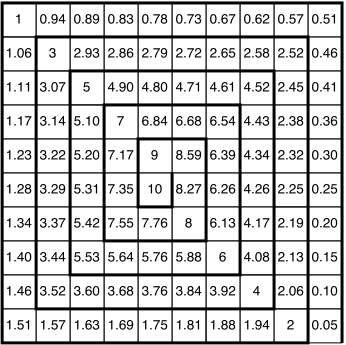
Abb. 21: Modifikation

Die Abbildung 22 zeigt das zugehörige Histogramm. Die Treppen werden nach oben immer steiler. Die letzte Stufe hat die Höhe 1.

Abb. 22: Histogramm

Für die Bodenkantenlänge 100 ergibt sich das Histogramm der Abbildung 23.

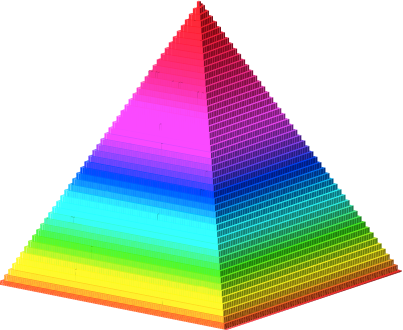
Abb. 23: Ulam-Pyramide