Hans Walser, [20180913]

Umfang- und flŠchengleiche Dreiecke

Anregung: Thomas Jahre, Chemnitz

1     Problemstellung

Gibt es zwei nicht kongruente Dreiecke, welche den gleichen Umfang und den gleichen FlŠcheninhalt haben?

2     Lšsung

Die beiden Dreiecke

 

 

a

b

c

Dreieck 1

20

24

16

Dreieck 2

22

23

15

Tab. 1: Die beiden Lšsungen

haben denselben Umfang U und denselben FlŠcheninhalt F:

 

                                                                             (1)

 

 

Die beiden Dreiecke sind aber nicht kongruent (Abb. 1).

Abb. 1: Die beiden Dreiecke

3     Visualisierung der beiden Gleichheiten

3.1    Umfanggleichheit

Abb. 2: Gleiche UmfŠnge

3.2    FlŠchengleichheit

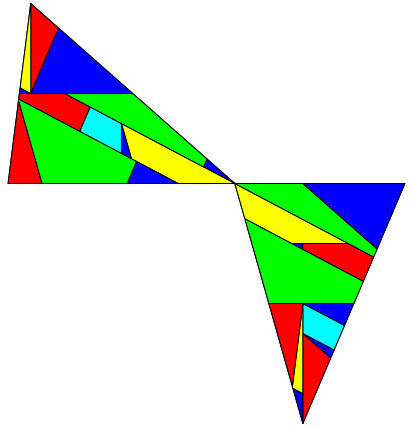
Abb. 3: Gleiche FlŠcheninhalte

4     Rechnerische Beweise

Zu einem Dreieck mit den Seiten a, b, c ist

 

                                                                                                               (2)

 

 

und:

 

                                         (3)

 

 

Wenn wir die Daten der Tabelle 1 einsetzen, erhalten wir fŸr beide Dreiecke dieselben Werte (1).

5     Wie kommt man auf so etwas?

Zu gegebenem Umfang U und FlŠcheninhalt F bilden (2) und (3) ein Gleichungssystem fŸr die Unbekannten a, b, c. Da wir drei Unbekannte, aber nur zwei Gleichungen haben, ist das System unterbestimmt. Wir kšnnen also fŸr eine der drei Unbekannten einen Wert wŠhlen und mit (2) und (3) die beiden anderen ausrechnen. Es gibt daher zu gegebenem U und F unendliche viele Lšsungen.

Ich habe die ganzzahligen Lšsungen der Tabelle 1 auf einer Bahnfahrt durch Probieren gefunden.

6     Spezielle Dreiecke

FŸr spezielle Dreiecke erhalten wir eine weitere Gleichung:

Gleichschenkliges Dreieck:

 

                                                                                                                             (4)

 

 

Rechtwinkliges Dreieck:

 

                                                                                                               (5)

 

 

In diesen FŠllen haben wir keinen Freiheitsgrad mehr. Es gibt im Prinzip nur eine Lšsung. Anders formuliert: Gleichschenklige Dreiecke oder rechtwinklige Dreiecke mit demselben Umfang und demselben FlŠcheninhalt sind kongruent.

FŸr sehr spezielle Dreiecke erhalten wir sogar zwei weitere Gleichungen:

Gleichseitiges Dreieck:

 

                                                                                                               (6)

 

 

Rechtwinklig gleichschenkliges Dreieck:

 

                                                                                                 (7)

 

 

In diesen FŠllen haben wir insgesamt ein Ÿberbestimmtes Gleichungssystem und in der Regel keine Lšsung.