Hans Walser, [20170919]

Umkehrung einer Folge

1 Worum geht es?

Die in [1] erscheinende Folge wird leicht verallgemeinert und dann umgekehrt laufen gelassen. Eine Spielerei, die Zeit zu vertreiben.

2 Die Folge

Für reelles c > 0 konvergiert Folge mit der Iteration

(1)

zum Grenzwert .

Es handelt sich hier um das Verfahren von Heron oder von Newton-Raphson.

Die Tabelle 1 zeigt das Beispiel für c = 3 und den Startwert a₀ = 100.

n	an
0	100
1	50.01500000
2	25.03749100
3	12.57865566
4	6.408577457
5	3.438350033
6	2.155430774
7	1.773631961
8	1.732538224
9	1.732050876
10	1.732050808
11	1.732050808

Tab. 1: Beispiel

Am Anfang werden die Folgenglieder praktisch halbiert.

Das heißt, dass sich die Folgenglieder praktisch verdoppeln, wenn wir die Folge umgekehrt laufen lassen. Als praktisch exponentielles Wachstum.

3 Umgekehrt ist auch gefahren

Aus (1) erhalten wir:

(2)

Wir fassen (2) als quadratische Gleichung für a_n auf und erhalten mit der Mitternachtsformel:

(3)

Aus (3) bilden wir die Umkehrfolgen b_n mit der Iteration:

(4)

Wegen dem ± in (4) haben wir es mit zwei Folgen zu tun.

Die Tabelle 2 zeigt für die plus-Variante von (4) das Beispiel mit c = 3 und dem Startwert b₀ = 5.

n	bn
0	5
1	9.690415760
2	19.22478294
3	38.37138261
4	76.70365365
5	153.3877490
6	306.7657185
7	613.5265472
8	1227.050650

Tab. 2: Umgekehrte Gangart

Wir sehen, wie sich die Folgenglieder praktisch verdoppeln.

Die Tabelle 3 zeigt die minus-Variante für dasselbe Beispiel.

n	bn
0	5
1	0.309584240
2	0.309584240 – 1.704158912i
3	0.0915653833 + 0.715726915i
4	0.05656054464 – 1.156465953i
5	0.02514520216 + 0.925648676i
6	0.01329259164 – 1.038106317i
7	0.006458942731 + 0.981184333i
8	0.003275354222 – 1.009466594i
9	0.001626089294 + 0.995281469i
10	0.0008159268205 – 1.002362947i
11	0.0004072410283 + 0.998819448i
12	0.0002038008793 – 1.000590506i
13	0.0001018553196 + 0.999704805i
14	0.00005093893620 – 1.000147612i
15	0.00002546664855 + 0.999926198i

Tab. 3: Minus-Variante

Wir erhalten komplexe Zahlen. Die Realteile halbieren sich praktisch. Die Imaginärteile streben gegen 1.

4 Illustrationen

Wir schreiben (4) in der Form einer Relation:

(5)

Für erhalten wir die Punkte der Abbildung 1.

Abb. 1: Hyperbel

Es handelt sich um eine Hyperbel. Die eine Asymptote ist die Gerade y = 2x, die andere die x-Achse.

Für wir die zweite Koordinate komplex.

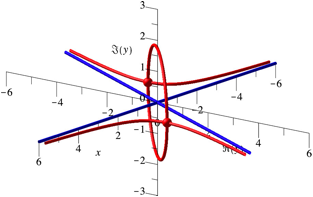
Wir arbeiten nun im Raum (Abb. 2). Die räumliche x-Achse bleibt die x-Achse. Orthogonal dazu arbeiten wir mit der Gaußschen Zahlenebene. Die Standard-y-Achse stellt den Realteil von dar, die Standard-z-Achse den Imaginärteil von .

.

Abb. 2: Im Raum

Die Abbildung 3 zeigt die Situation in der Sicht von oben. Bis auf den komplexen Teil entspricht das der Abbildung 1.

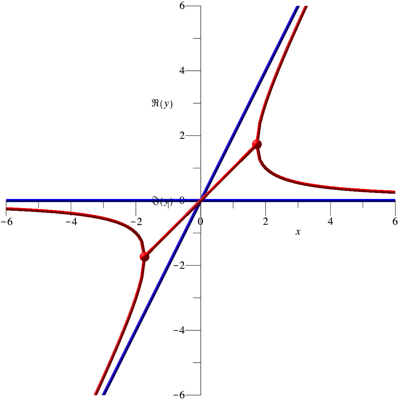
Abb. 3: Sicht von oben

Die Abbildung 4 zeigt die Sicht von vorne, in der Gegenrichtung zur reellen y-Achse. Der komplexe Teil erscheint als Kreis mit dem Radius .

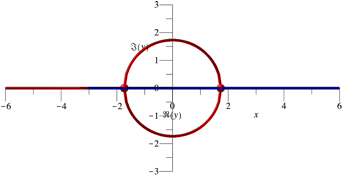
Abb. 4: Sicht von vorne

In Wirklichkeit ist der komplexe Teil aber eine Ellipse mit dem Achsenverhältnis (Abb. 5).

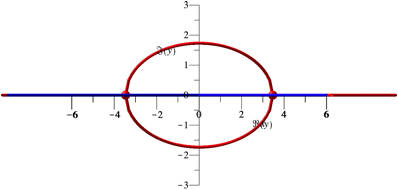
Abb. 5: Wahre Gestalt der Ellipse

Websites

[1] Hans Walser: Quadratur des Rechtecks (abgerufen 20.09.2017):

www.walser-h-m.ch/hans/Miniaturen/Q/Quadratur_des_Rechtecks/Quadratur_des_Rechtecks.htm