Hans Walser, [20101225b]
Umrechtecke der Ellipse
1
Worum es geht
Wir umschreiben einer
Ellipse Rechtecke in verschiedenen Positionen.
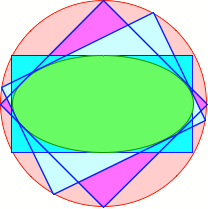
Umrechtecke
Wir vermuten, dass die
Ecken dieser Rechtecke alle auf demselben Kreis liegen. Dieser Kreis hat den
Radius 
, wobei a und b die Halbachsen der Ellipse bezeichnen.
Verifikation durch DGS.
2
Eine Rosette
Wir zeichnen nun in den
Berźhrungspunkten der Rechtecke die Lote zu den Rechtecksseiten ein. Der
Schnittpunkt dieser Lote beschreibt eine Rosette.
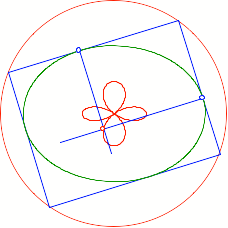
Rosette
3
Hyperbel
Bei einer Hyperbel mit 
ergibt sich eine
analoge Situation. Der Kreisradius ist nun 
.
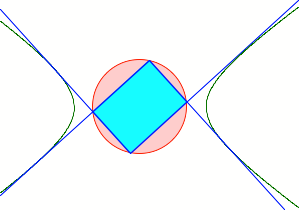
Hyperbel