Hans Walser, [20200719]
Umsechseck
Anregung: M. E., B.
1 Erinnerung: Kantenmittenviereck
Das Kantenmittenviereck eines beliebigen Vierecks ist ein Parallelogramm (Satz von Varignon). Umgekehrt gibt es zu einem gegebenen Parallelogramm unendlich viele passende Umvierecke.
2 Problemstellung
Wie ist es beim Sechseck?
3 Kantenmittensechseck
Dem Sechseck R0R1...R5 (Abb. 1a) wird das Kantenmittensechseck A0A1...A5 einbeschrieben (Abb. 1b).
Welche Eigenschaften hat das Kantenmittensechseck?
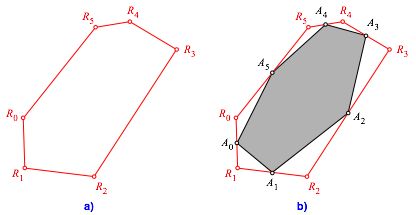
Abb. 1: Sechseck und Kantenmittensechseck
4 Strahlensatz und Vektoren
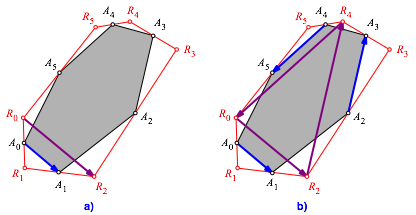
Abb. 2: Strahlensatz und Vektoren
Auf Grund des Strahlensatzes (Zentrum R1, Abb. 2a) ist:
![]() (1)
(1)
Analog (Abb. 2b):
![]() (2)
(2)
Daher ist:
![]() (3)
(3)
Daraus ergibt sich:
![]() (4)
(4)
Die drei blauen Vektoren bilden also ein Dreieck (Abb. 3b). Ebenso bilden die drei anderen Seiten parallel verschoben ein Dreieck (Abb. 3c).
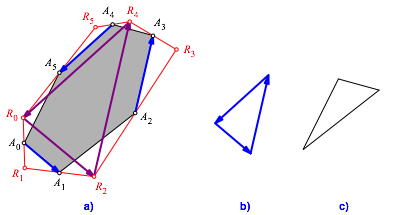
Abb. 3: Dreiecke
Wenn die Bedingung (4) nicht erfźllt ist, kann das Sechseck A0A1...A5 kein Umsechseck haben, denn aus der Existenz eines Umsechsecks folgt automatisch (4).
Die Bedingung (4) kennzeichnet also die Kantenmittensechsecke.
5 Weitere Umsechsecke
Wenn wir die Ecken des Umsechseckes R0R1...R5 alternierend um einen Vektor und seinen Gegenvektor verschieben (Abb. 4a), erhalten wir ein Sechseck mit demselben Kantenmittensechseck (Abb. 4b).
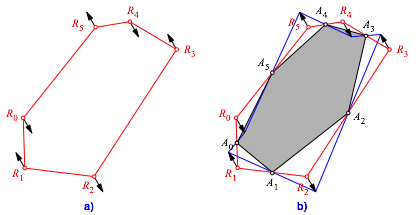
Abb. 4: Alternierendes Verschieben der Ecken
Dies ergibt sich unmittelbar aus den Strahlensatz.
Ein Kantenmittensechseck hat also beliebig viele Umsechsecke.
6 Zusammenfassung
Ein Sechseck A0A1...A5 ist genau dann ein Kantenmittensechseck, wenn es die Bedingung (4) erfźllt. In diesem Fall hat es unendlich viele passende Umsechsecke.
7 Link mit dem Satz von Varignon
Die zu (4) analoge Bedingung fźr ein Viereck A0A1A2A3 lautet:
![]() (5)
(5)
Der zweite Vektor ist also der Gegenvektor zum ersten. Er ist gleich lang und antiparallel. Das hei§t, dass das Viereck A0A1A2A3 ein Parallelogramm ist (Abb. 5).
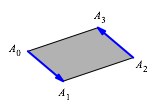
Abb. 5: Parallelogramm
8 Verallgemeinerung
Ein Achteck A0A1...A7 ist genau dann ein Kantenmittenachteck, wenn es die Bedingung
![]() (6)
(6)
erfźllt. Es hat unendlich viele Umachtecke.
Ein 2n-Eck ist genau dann ein Kantenmitten-2n-Eck, wenn es die Bedingung
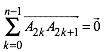 (7)
(7)
erfźllt. Es hat unendlich viele Um-2n-Ecke.
Websites
Hans Walser: Umviereck
http://www.walser-h-m.ch/hans/Miniaturen/U/Umviereck/Umviereck.htm
Hans Walser: Logarithmische Kantenmittenspirale
www.walser-h-m.ch/hans/Miniaturen/L/Log_Kantenmittenspirale/Log_Kantenmittenspirale.htm
Hans Walser: Logarithmische Kantenmittenspiralen
www.walser-h-m.ch/hans/Miniaturen/L/Log_Kantenmittenspiralen/Log_Kantenmittenspiralen.htm
Hans Walser: Spiralen im regelmŠ§igen Vieleck
www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm
Hans Walser: Kantenmittenspirale
www.walser-h-m.ch/hans/Miniaturen/K/Kantenmittenspirale/Kantenmittenspirale.htm