Hans Walser, [20170123a]
Ungerade mal ungerade
1 Schule
In der Schule lernt man, dass das Produkt zweier ungerader Zahlen eine ungerade Zahl ist.
Bewiesen
wird das formal: Eine ungerade Zahl lŠsst sich in der Form ![]() schreiben.
Daher wird:
schreiben.
Daher wird:
![]() (1)
(1)
2 Mit dem Finger
Es geht aber einfacher.
Wenn wir eine ungerade Anzahl von Objekten in eine Reihe auslegen, gibt es ein Objekt in der Mitte (Abb. 1). Wir kšnnen den Finger drauflegen.
![]()
Abb. 1: Kreis in der Mitte
Bei einer nicht zu gro§en Anzahl erkennen wir dieses mittlere Objekt sofort, wir brauchen nicht zu zŠhlen. Die Abbildung 2 zeigt zwei ăfalscheŇ Beispiele.
![]()
Abb. 2: Falsche Beispiele
In der Abbildung 3 haben wir eine rechteckige Anordnung. In der horizontalen Richtung ist die Anzahl ungerade, ebenso in der vertikalen Richtung.
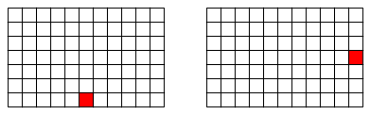
Abb. 3: Horizontal und vertikal ungerade
Daher gibt es ein Objekt genau in der Mitte des Rechteckes. Wir kšnnen den Finger auf dieses Objekt legen (Abb. 4).

Abb. 4: Objekt in der Mitte
Zu allen źbrigen Objekten gibt es ein Gegenstźck (exemplarisch blau in Abb. 4). Die Anzahl der źbrigen Objekte ist also gerade. Zusammen mit dem Objekt in der Mitte ergibt sich eine ungerade Anzahl.
3 Nochmals Schule
Es geht auch formal (gut geordnet ist halb gelšst):
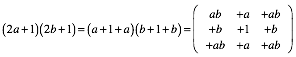 (2)
(2)