Hans Walser, [20150912]

Unterteilung des Tangentenvierecks

Anregung: M. M., O.

1     Worum geht es?

Die Triangulation eines Tangentenvierecks fŸhrt zu speziellen BerŸhrungspunkten der Inkreise der Teildreiecke.

2     Beliebiges Viereck

ZunŠchst zerlegen wir ein beliebiges Viereck mit einer Diagonalen in zwei Dreiecke und zeichnen in jedem Teildreieck den Inkreis. Die beiden Inkreise berŸhren die Diagonale in der Regel in verschiedenen Punkten (Abb. 1).

 

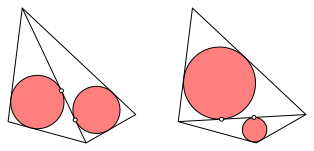
Abb. 1: Inkreise in Teildreiecken

 

Wir vermuten, dass die Distanz zwischen den beiden BerŸhrungspunkten unabhŠngig davon ist, mit welcher Diagonalen wir das Viereck unterteilt haben.

Zur Berechnung dieser Distanz  verwenden wir die Bezeichnungen der Abbildung 2.

 

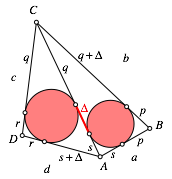
Abb. 2: Bezeichnungen

 

Wir berechnen die alternierende Seitensumme des Viereckes ABCD:

 

                                     (1)

 

Somit ist:

 

                                                                                                           (2)

 

Die Distanz  ist also unabhŠngig von der zur Unterteilung gewŠhlten Diagonalen.

3     Tangentenviereck

In einem Tangentenviereck ist die alternierende Seitensumme null. Daher ist auch , und die beiden Inkreise in den Teildreiecken haben den BerŸhrungspunkt mit der Diagonalen gemeinsam (Abb. 3).

 

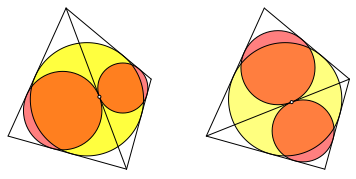
Abb. 3: Tangentenviereck

 

4     Umgekehrte Sicht

Wir beginnen mit zwei sich berŸhrenden Kreisen und wŠhlen auf der gemeinsamen Tangente im BerŸhrungspunkt zwei Punkte. Von diesen Punkten aus zeichnen wir je die anderen Tangenten an die beiden Kreise und erhalten so ein Tangentenviereck (Abb. 4).

 

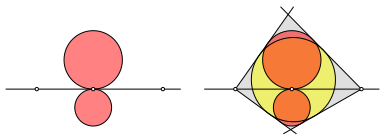
Abb. 4: Konstruktion eines Tangentenviereckes

 

Werden die beiden Punkte auf der gleichen Seite gewŠhlt, ergibt sich ein nicht konvexes Viereck mit Ankreis (Abb. 5). Da der Ankreis auch alle vier Seitengeraden des Viereckes berŸhrt, kann das Viereck ebenfalls als Tangentenviereck bezeichnet werden.

 

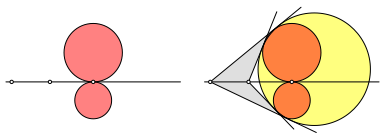
Abb. 5: Ankreis

 

In einem nicht konvexen Tangentenviereck ist die doppelt alternierende Seitensumme null. Dazu die Bezeichnungen der Abbildung 6.

 

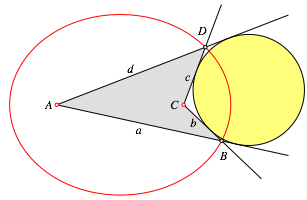
Abb. 6: Nicht konvexes Tangentenviereck

 

Es ist:

 

                                                                                                         (3)

 

Das hei§t aber, dass die Punkte B und D auf derselben Ellipse mit den Brennpunkten A und C liegen.

Schlie§lich kšnnen wir die beiden Kreise ineinander zeichnen (Abb. 7 und 8).

 

Abb. 7: Kreise berŸhren sich von innen

 

Abb. 8: Kreise berŸhren sich von innen