Hans Walser, [20240415]

Unterteilung durch Falten

1 Worum es geht

Falten. Flächenanteile

2 Falten

Wir falten bei einem DIN A4-Papier die rechte untere Ecke auf die linke obere Ecke (Abb. 1) und zurück. Anschließend falten wir die rechte obere Ecke auf die linke untere Ecke und zurück. Die Faltlinien ergeben zwei gleichschenklige Dreiecke.

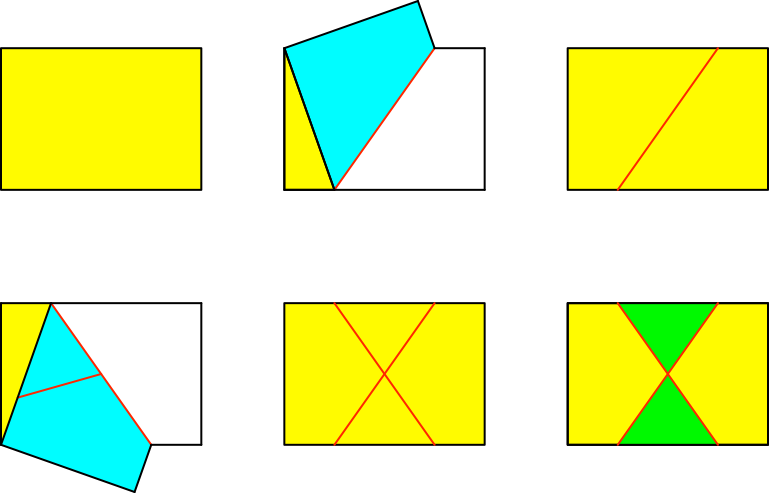
Abb. 1: Falten. Gleichschenklige Dreiecke

3 Problemstellung

Wie groß ist der Flächenanteil der beiden gleichschenkligen Dreiecke an der Gesamtfläche des Rechteckes?

4 Faltlösungen

Über die Gültigkeit von Faltlösungen kann man streiten.

4.1 Erste Faltlösung

Wir falten das DIN A4-Papier zu DIN A5 (Abb. 2), dann zu DIN A6 und schließlich zu DIN A7.

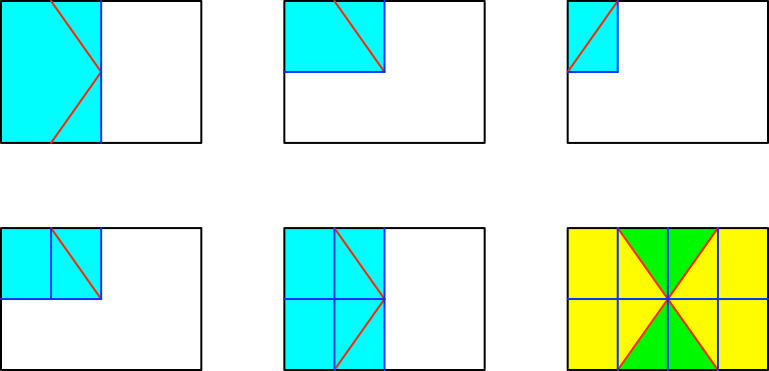
Abb. 2: DIN A4 > DIN A5 > DIN A6 > DIN A7

Dann falten wir wieder auf. Wir haben nun acht Teilrechtecke, vier davon sind durch die gleichschenkligen Dreiecke zur Hälfte belegt. Also 4*½*1/8 = ¼.

4.2 Zweite Faltlösung

Wir falten von jeder Seite her bis zur Mitte.

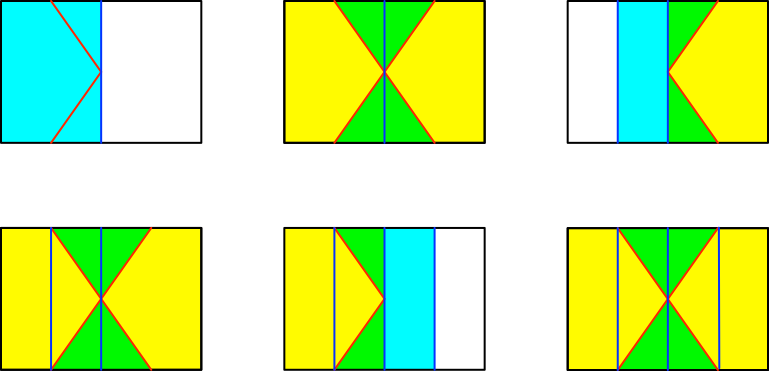
Abb. 3: Fenster schließen

Dann falten wir wieder auf. Die grünen gleichschenkligen Dreiecke machen die Hälfte der Hälfte aus, also einen Viertel.

5 Bearbeitung

Nun also ernsthaft.

Wir arbeiten allgemein mit einem Rechteck der Länge a und der Breite 1 (Abb. 4).

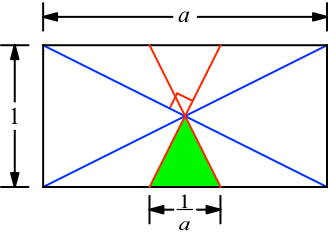
Abb. 4: Allgemeines Rechteck

Die beiden Diagonalen haben die Steigungen –1/a und 1/a. Die Faltlinien sind die Mittelsenkrechten der Diagonalen und haben daher die Steigungen a beziehungsweise –a.

Die gleichschenkligen Dreiecke haben die Höhe ½ und wegen der Steigung der Schenkel die Basislänge 1/a. Die Summe der Flächeninhalte der beiden gleichschenkligen Dreiecke ist daher ½*1/a.

Das Rechteck hat den Flächeninhalt a. Der Flächenanteil der beiden gleichschenkligen Dreiecke im Vergleich zur Rechteckfläche ist somit ½*1/a².

In einem Rechteck im DIN-Format ist a = √2 ≈ 1.414. Der Flächenanteil der beiden gleichschenkligen Dreiecke ist in diesem Fall ¼. Die Zerlegung der Abbildung 3 illustriert diesen Sachverhalt. Der Flächenanteil ¼ der beiden gleichschenkligen Dreiecke kann durch Abzählen der ganzen und halben gleichschenkligen Dreiecke bestätigt werden.

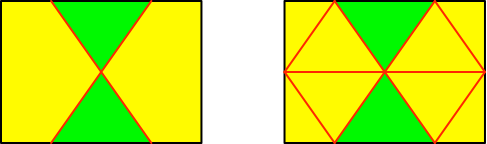
Abb. 5: Zerlegung

6 Diskussion

Für a = 1 (Quadrat, Abb. 6) ist der Flächenanteil ½.

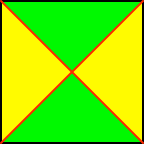
Abb. 6: Quadrat

Für a = √2 (DIN-Format, Abb. 5) ist der Flächenanteil ¼.

Für a = √3 (Abb. 7) ist der Flächenanteil ⅙.

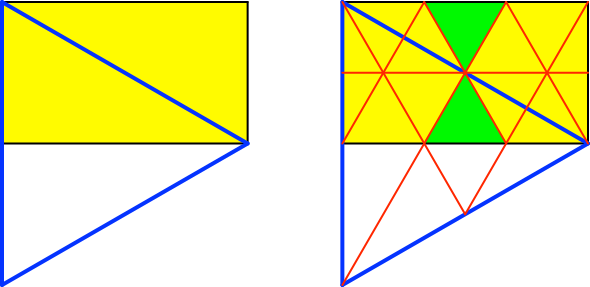
Abb. 7: Am gleichseitigen Dreieck

Für a = √4 = 2 (doppeltes Quadrat, Abb. 8) erhalten wir den Flächenanteil ⅛.

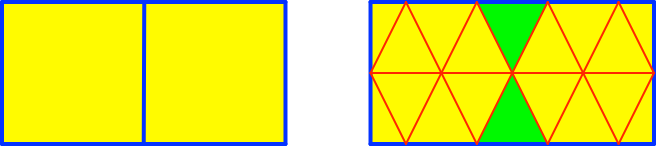
Abb. 8: Doppeltes Quadrat

Für a = √5 ≈ 2.236 (Abb. 9) erhalten wir den Flächenanteil 1/10.

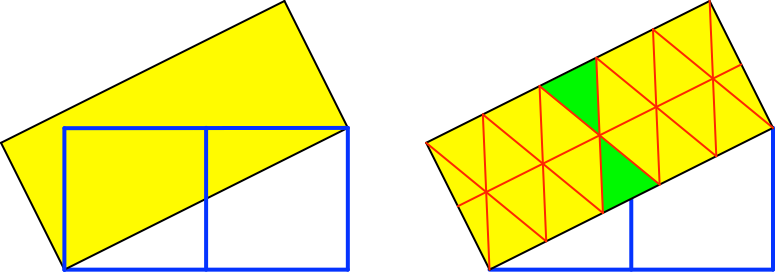
Abb. 9: √5

7 Der Weg in die Abstraktion

Für a < 1 reichen die gleichschenkligen Dreiecke über das Rechteck hinaus (Abb. 10 für a = ½). Mit einem realen Papierrechteck ist dies nicht zu machen. Wir müssen auf die zeichnerische Abstraktion ausweichen.

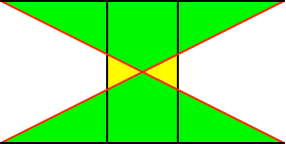
Abb. 10: Rechteck zu klein

Nach unserer Rechnung ist für a = ½ die Flächensumme der gleichschenkligen Dreiecke doppelt so groß wie das Rechteck. Das heißt, dass ein einzelnes der beiden gleichschenkligen Dreiecke denselben Flächeninhalt hat wie das Rechteck. Dies kann mit einer gemeinsamen Zerlegung illustriert werden (Abb. 11).

Abb. 11: Flächengleichheit eines Dreiecks mit dem Rechteck

8 Sonderfall

Für die Flächengleichheit der Summe der beiden gleichschenkligen Dreiecke mit dem Rechteck erhalten wir die Bedingung:

½*1/a² = 1

Daraus folgt a = √(½) ≈ 0.707 (Abb. 12). Das Rechteck hat ebenfalls ein DIN-Format, steht aber im Hochformat.

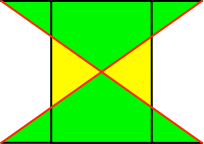
Abb. 12: DIN-Format im Hochformat

Die Abbildungen 13 und 14 illustrieren die Flächengleichheit.

Abb. 13: Flächengleichheit

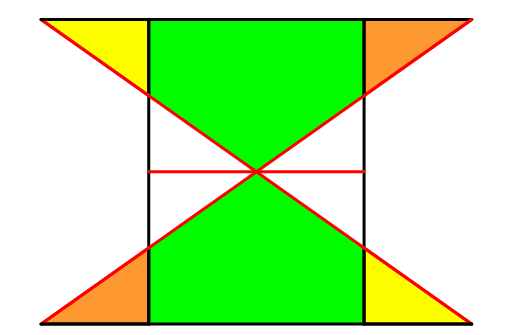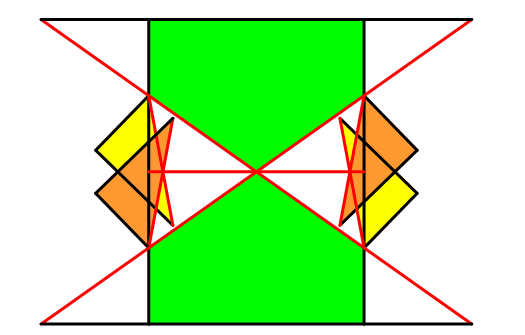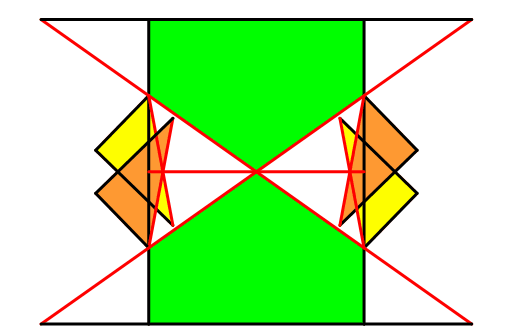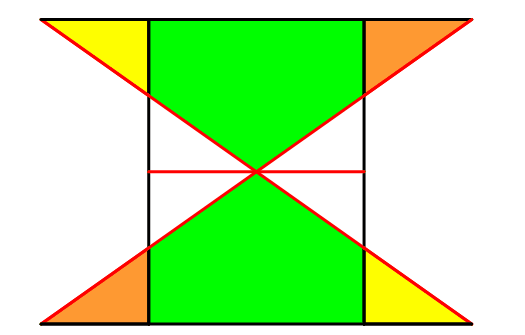
Abb. 14: Flächengleichheit