Hans Walser, [20171007]

Unterteilung mit Höhen

Anregung: Hölzl (2017)

1 Worum geht es?

Wir unterteilen ein Rechteck mit einer Diagonalen in zwei rechtwinklige Dreiecke. Jedes Dreieck unterteilen wir fortlaufend mit den Hypotenusenhöhen in weitere rechtwinklige Dreiecke.

Gesucht ist eine „schöne“ Gesamtfigur.

2 Einstieg

Wir beginnen mit einem Rechteck mit dem Seitenverhältnis 3:4 und einer Diagonalen (Abb. 1a). Dann unterteilen wir jedes Teildreieck mit seiner Hypotenusenhöhe (Abb. 1b). Wir iterieren den Unterteilungsprozess (Abb. 1c und 1d).

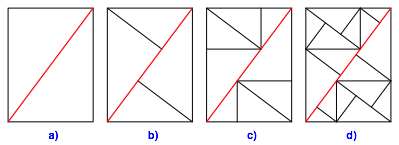
Abb. 1: Seitenverhältnis 3:4

Die beiden Teilfiguren oberhalb und unterhalb der Diagonalen haben keine Punkte auf der Diagonale gemeinsam. Die Abbildung 2 zeigt die Situation nach siebenmaligem Unterteilen. Auch hier keine gemeinsamen Punkte.

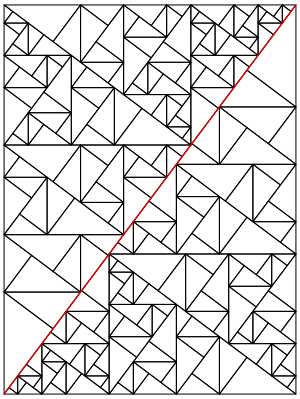
Abb. 2: Siebenmaliges Unterteilen

3 Quadrat als triviale Lösung

Für das Quadrat erhalten wir die triviale Lösung der Abbildung 3.

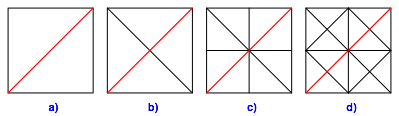
Abb. 3: Quadrat als triviale Lösung

4 Eine Lösung

Mit einiger Rechnung finden wir eine Lösung: das Rechteck mit dem Seitenverhältnis:

(1)

Dabei ist der goldene Schnitt (Walser 2013a). Das Rechteck der Abbildung 4 ist allerdings nicht das übliche goldene Rechteck. Das Seitenverhältnis ist wegen (1) nicht der goldene Schnitt, hingegen stehen die kurze Seite und die Diagonale im Verhältnis des goldenen Schnittes.

Die Abbildung 4 zeigt die ersten Schritte der Unterteilung. In der Abbildung 4d sehen wir zum ersten Mal durchgehende Linien.

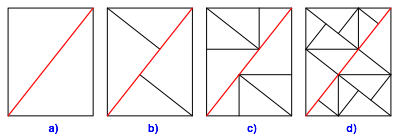
Abb. 4: Nichttriviale Lösung

Die Abbildungen 5 bis 8 zeigen die vier folgenden Schritte. Gleich große Dreiecke sind in derselben Farbe ausgemalt.

Abb. 5: Vierte Unterteilung

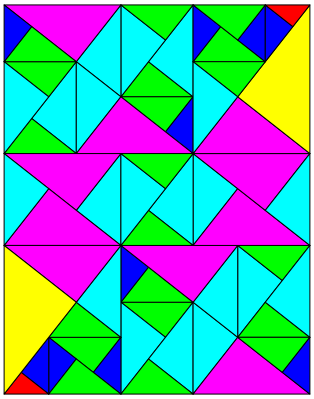
Abb. 6: Fünfte Unterteilung

Abb. 7: Sechste Unterteilung

Bei der siebten Unterteilung (Abb. 8) ist die geneigte Leserin eingeladen, selber zu den Farbstiften zu greifen. Wie viele Farben braucht es? Wie viele Dreiecke hat es von jeder Farbe (vgl. Glötzner 2017)?

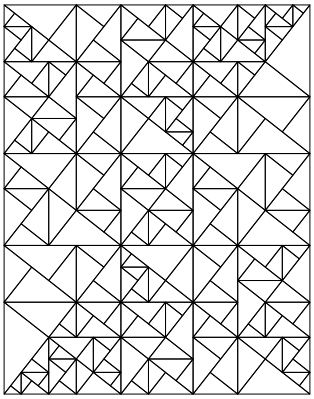
Abb. 8: Siebente Unterteilung

5 Die Rechnung

Wir wollen den Sachverhalt (1) herleiten. Dazu verwenden wir die Bezeichnungen der Abbildung 9a. Weiter verwenden wir die relativen Höhenabschnitte:

(2)

Es ist dann:

(3)

Damit finden wir die Maße der Abbildung 9b.

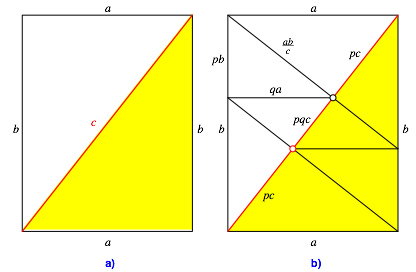
Abb. 9: Berechnungen

Die Treffpunktbedingung (roter Punkt) lautet:

(4)

Zusammen mit (3) ergibt sich die quadratische Gleichung für p:

(5)

Wegen 0 < p < 1 erhalten wir die Lösung:

(6)

Aus (2) ergibt sich:

(7)

Damit ist (1) nachgewiesen.

6 Eine weitere Lösung

Mit einer analogen Rechnung finden wir eine weitere Lösung (der Treffpunkt ist nun in der Mitte):

(8)

Die Abbildung 10 zeigt die ersten Schritte.

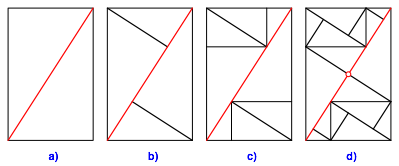
Abb. 10: Erste Schritte

Mit dem Auftreten von sind wir im Prinzip im Bereich des DIN-Formates (Walser 2013b). Das Rechteck der Abbildung 10 ist allerdings nicht direkt im DIN-Format.

Die Abbildungen 11-## zeigen weitere Schritte.

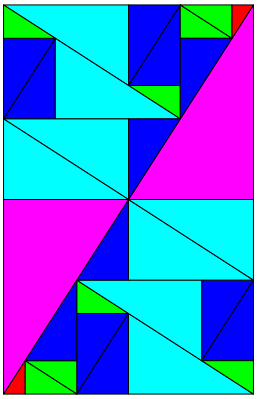
Abb. 11: Vierte Unterteilung

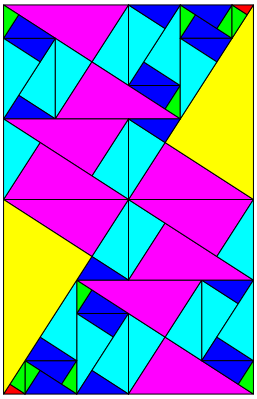
Abb. 12: Fünfte Unterteilung

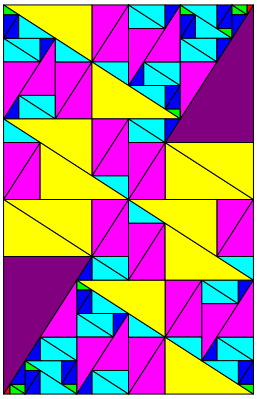
Abb. 13: Sechste Unterteilung

Bei der siebten Unterteilung (Abb. 14) ist die geneigte Leserin eingeladen, selber zu den Farbstiften zu greifen. Wie viele Farben braucht es? Wie viele Dreiecke hat es von jeder Farbe?

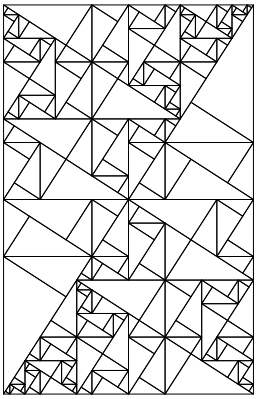
Abb. 14: Siebte Unterteilung

Literatur

Glötzner, Fabian (2017): Binomialverteilung erkunden. Beispiele untersuchen, systematisieren und erweitern. mathematik lehren 201 | 2017, 36-41.

Hölzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und Zusammenhänge findest du? mathematik lehren 201 | 2017, 12-15.

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Websites

[1] Hans Walser: Dreiecksunterteilung und Binomialverteilung (abgerufen 3.9.2017):

www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung2/Dreiecksunterteilung2.htm