Hans Walser, [20210207]
Varignon
1 Worum geht es?
Variante zum Satz von Varignon. €hnliche Rhomben
2 Der Satz von Varignon
Der Satz von Varignon besagt, dass das Seitenmittenviereck eines beliebigen Viereckes ein Parallelogramm ist (Abb. 1).
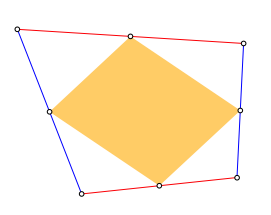
Abb. 1: Parallelogramm von Varignon
3 Viereck aus Rhomben
Wir bauen ein Viereck aus Šhnlichen Rhomben (Abb. 2).
Abb. 2: Viereck aus Rhomben
Wir kšnnen auf zwei Arten ein Parallelogramm einpassen (Abb. 3).
Abb. 3.1: Erstes Parallelogramm
Abb. 3.2: Zweites Parallelogramm
4 Beweis
Rechnerische Beweise.
Die €hnlichkeit der Rhomben wird durch das DiagonalenverhŠltnis v definiert.
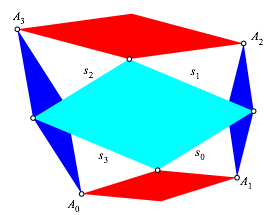
Abb. 4.1: Bezeichnungen fźr die erste Lšsung
Wir setzen:
(1)
Damit erhalten wir fźr die SeitenlŠngen des eingepassten Viereckes:
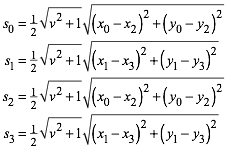(2)
Je zwei gegenźberliegende Seiten sind gleich lang. Die erste Lšsung (Abb. 4.1) also ist ein Parallelogramm.
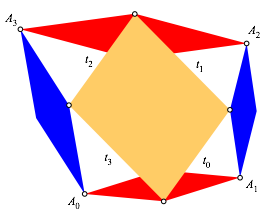
Abb. 4.2: Zweite Lšsung
Fźr die zweite Lšsung (Abb. 4.2) erhalten wir:
(3)
Wir haben ebenfalls ein Parallelogramm.
Die beiden Parallelogramme haben dieselben SeitenlŠngen. Ihre Winkel sind aber unterschiedlich.
Die
SeitenlŠngen sind bis auf den Faktor 
die halben
DiagonalenlŠngen des Startviereckes. Fźr v
= 0 erhalten wir den klassischen Satz von Varignon.
5 Sonderfall
Fźr v = 1 sind die Rhomben Quadrate (Abb. 5).
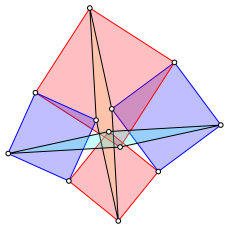
Abb. 5: Sonderfall Quadrate
In diesem Sonderfall sind die beiden Parallelogramme kongruent (Beweis rechnerisch).
Website
Hans
Walser: Rhomben
http://www.walser-h-m.ch/hans/Miniaturen/R/Rhomben3/Rhomben3.htm