Hans Walser, [20210208]

Varignon

1 Worum geht es?

Variationen um den Satz von Varignon

2 Der Satz von Varignon

Nach dem Satz von Varignon bilden die Seitenmitten eines beliebigen Viereckes ein Parallelogramm(Abb. 1). Die Seiten des Parallelogramms sind parallel zu den Diagonalen und halb so lang. Beweis mit Strahlensätzen.

Die Winkel des Varignon-Parallelogramms sind gleich den Diagonalenschnittwinkeln.

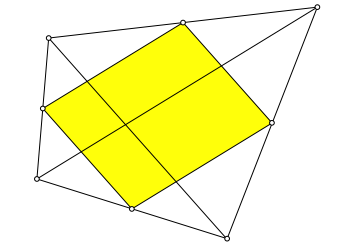
Abb. 1: Satz von Varignon

3 Gleichschenklige Dreiecke ansetzen

Wir setzen den Seiten des Viereckes ähnliche gleichschenklige Dreiecke an, alternierend nach innen und außen (Abb. 2).

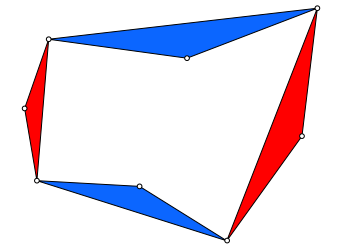
Abb. 2: Ähnliche gleichschenklige Dreiecke

Die Spitzen der gleichschenkligen Dreiecke bilden nun ebenfalls ein Parallelogramm (Abb. 3).

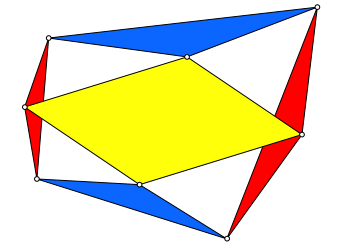
Abb. 3: Neues Parallelogramm

4 Beweis

Wir vergleichen unser Viereck C₀C₁C₂C₃ mit dem Varignon-Parallelogramm B₀B₁B₂B₃ (Abb. 4).

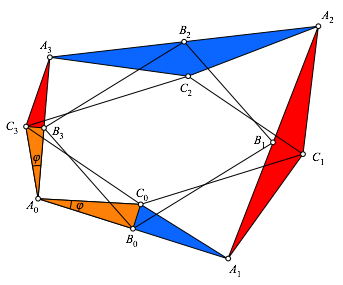
Abb. 4: Beweisfigur

Wir können die Strecke B₀B₃ mit einer Drehstreckung auf die Strecke C₀C₃ abbilden. Das Zentrum der Drehstreckung ist A₀, der Drehwinkel ist der Basiswinkel der gleichschenkligen Dreiecke und der Streckfaktor ist das Seitenverhältnis der Strecken A₀C₀ zu A₀B₀, also . Analog können wir die übrigen drei Seiten des Viereckes C₀C₁C₂C₃ durch Drehstreckungen aus den Seiten des Varignon-Parallelogramm B₀B₁B₂B₃ erhalten. Die Seiten des Viereckes C₀C₁C₂C₃ sind also proportional zu denen des Varignon-Parallelogramms. Das Viereck C₀C₁C₂C₃ ist daher auch ein Parallelogramm. Dies war zu zeigen.

Der spitze Winkel C₀C₃C₂ ist um kleiner als der entsprechende Winkel B₀B₃B₂ des Varignon-Parallelogramms und damit auch um kleiner als der spitze Diagonalenschnittwinkel.

Der stumpfe Winkel des neuen Parallelogramms ist entsprechend größer als der stumpfe Winkel des Varignon-Parallelogramms.

5 Zweite Lösung

Durch Vertauschen der Begriffe innen und außen erhalten wir mit denselben gleichschenkligen Dreiecken ein zweites Parallelogramm (Abb. 5).

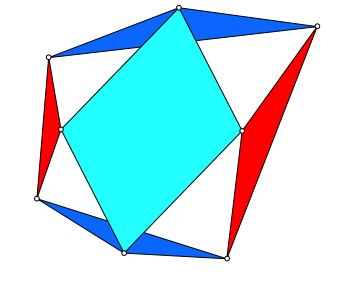
Abb. 5: Zweite Lösung

Die beiden Lösungen haben dieselben Seitenlängen, aber im Regelfall nicht dieselben Winkel. Die Winkel unterscheiden sich um .

6 Sonderfälle

Die Sonderfälle ergeben sich durch spezielle gleichschenklige Dreiecke.

6.1 Gleichseitige Dreiecke

Bei gleichseitigen Dreiecken ist und damit der Streckfaktor . Die Seiten des neuen Parallelogramms sind also doppelt so lang wie jene des Varignon-Parallelogramms und damit gleich lang wie die Diagonalen des Ausgangsviereckes (Abb. 6). Wir können die Diagonalen direkt mit einer Drehung um 60° (ohne Streckung) auf die Seiten des neuen Parallelogramms abbilden.

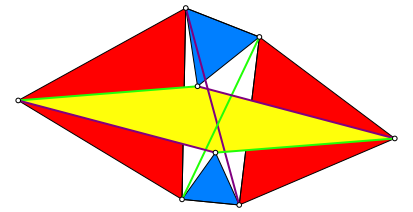
Abb. 6: Gleichseitige Dreiecke

6.2 Halbe Quadrate

Wir setzen rechtwinklig gleichschenklige Dreiecke an, halbe Quadrate also, und zeichnen die beiden Fälle, die sich durch Vertauschen von innen und außen ergeben (Abb. 7).

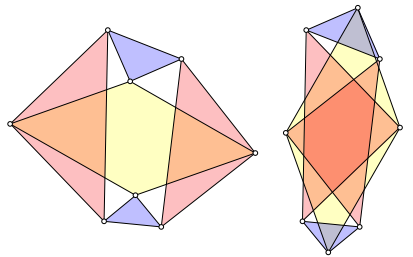
Abb. 7: Kongruente Parallelogramme

In diesem Sonderfall ist und damit die Winkeldifferenz der beiden Parallelogramme . Dies hat zur Folge, dass die beiden Parallelogramme kongruent sind und durch eine Drehung im 90° auseinander hervorgehen.

6.3 Fünfpunkte-Geraden

Wir zeichnen im Ausgangsviereck die Diagonalen und dann die vier Kreise, die je durch zwei benachbarte Ecken und den Diagonalenschnittpunkt verlaufen (Abb. 8).

Abb. 8: Vier Kreise

Und nun passen wir gleichschenklige Dreiecke ein gemäß Abbildung 9. Aus Kreiswinkelsätzen (Sehnenvierecke) folgt, dass der Basiswinkel dieser gleichschenkligen Dreiecke die Hälfte des (in unserer Abbildung spitzen) Diagonalenschnittwinkels ist.

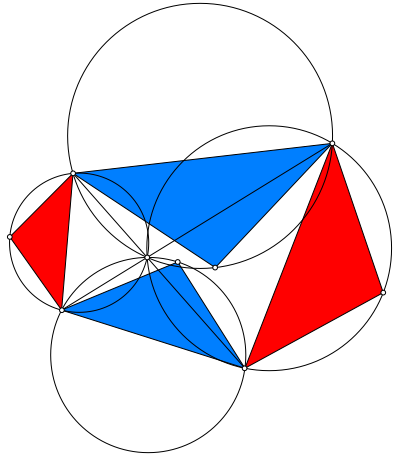
Abb. 9: Gleichschenklige Dreiecke

Die gleichschenkligen Dreiecke sind also ähnlich. Ihre Spitzen sind die Ecken eines Parallelogramms. Der spitze Winkel dieses Parallelogramms ist der um reduzierte Diagonalenschnittwinkel. Also null. Das Parallelogramm klappt zu einer Strecke zusammen (Abb. 10). Die vier Spitzen der gleichschenkligen Dreiecke liegen auf einer Geraden. Diese Gerade hat die Richtung der Winkelhalbierenden des spitzen Diagonalenschnittwinkels.

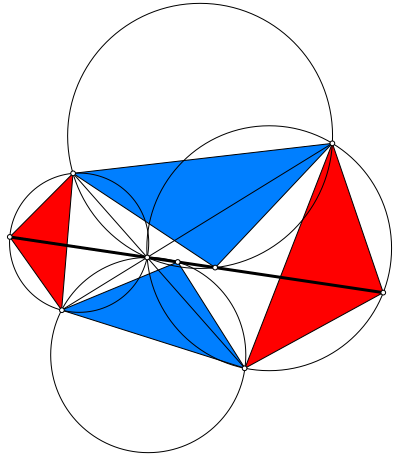
Abb. 10: Zusammengeklapptes Parallelogramm

Auf Grund der Abbildung 10 vermuten wir, dass auch der Diagonalenschnittpunkt auf dieser Geraden liegt. Dies kann wie folgt eingesehen werden.

Wir ergänzen die Kreisfigur der Abbildung 8 neu gemäß Abbildung 11 mit gleichschenkligen Dreiecken. Diese sind wieder ähnlich, allerdings nicht ähnlich zu den Dreiecken der Abbildungen 9 und 10. Ihr Basiswinkel ist nun nämlich die Hälfte des stumpfen Diagonalenschnittwinkels.

Analog wie oben folgt nun, dass die vier Spitzen der gleichschenkligen Dreiecke ebenfalls ein zusammengeklapptes Parallelogramm bilden. Sie liegen auf einer Geraden in der Richtung der Winkelhalbierenden des stumpfen Diagonalenschnittwinkels.

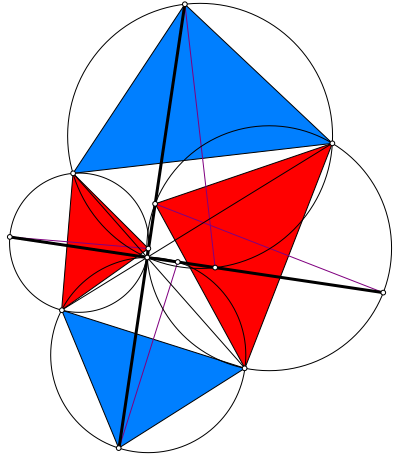
Abb. 11: Noch ein zusammengeklapptes Parallelogramm

Die Geraden der beiden zusammengeklappten Parallelogramme sind also orthogonal. Bei jedem der vier Kreise verlaufen sie durch je zwei diametrale Punkte. Ihr Schnittpunkt muss daher auf jedem der vier Kreise liegen, mithin im gemeinsamen Punkt der vier Kreise, also dem Diagonalenschnittpunkt.

Die beiden Geraden sind die Winkelhalbierenden der beiden Diagonalenschnittwinkel. Wir haben zwei Fünfpunkte-Geraden. Etwas für die Sammlung der kollinearen Punkte.

Websites

Hans Walser: Schlussstriche

http://www.walser-h-m.ch/hans/Schlussstriche/

Hans Walser: Varignon
http://www.walser-h-m.ch/hans/Miniaturen/V/Varignon3/Varignon3.htm

Hans Walser: Varignon
http://www.walser-h-m.ch/hans/Miniaturen/V/Varignon/Varignon.htm