Hans Walser, [20210208]
Varignon
1 Worum geht es?
Variante zum Satz von Varignon
2 Der Satz von Varignon
Nach dem Satz von Varignon bilden die Kantenmitten eines beliebigen Viereckes ein Parallelogramm (Abb. 1). Die Parallelogrammseiten sind parallel zu den Diagonalen des Ausgangsviereckes und halb solang.
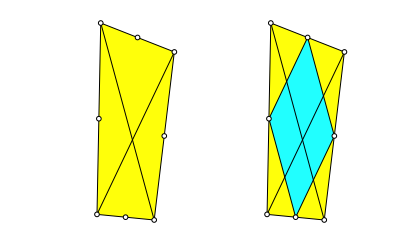
Abb. 1: Satz von Varignon
3 Variante
Wir setzen den Viereckseiten alternierend nach innen und nach au§en gerichtete gleichseitige Dreiecke an (Abb. 2).
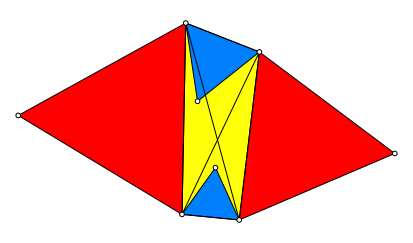
Abb. 2: Gleichseitige Dreiecke ansetzen
Die freien Ecken dieser gleichseitigen Dreiecke bilden ein Parallelogramm (Abb. 3). Seine Seiten sind gleich lang wie die Diagonalen des Ausgangsviereckes.
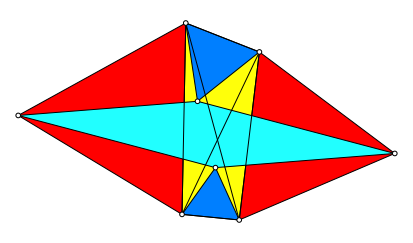
Abb. 3: Parallelogramm
4 Beweis
Wir verwenden die Bezeichnungen der Abbildung 4.
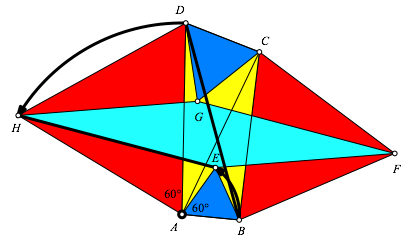
Abb. 4: Beweisfigur
Die Diagonale BD kann durch eine Drehung um den Punkt A um 60ˇ auf die Parallelogrammseite EH abgebildet werden. Analog fźr die anderen Parallelogrammseiten mit Drehungen um ±60ˇ um die restlichen Ecken des Ausgangsviereckes.
Die Parallelogrammseiten sind nicht mehr parallel zu den Diagonalen, sondern um ±60ˇ verdreht.
5 Zweite Lšsung
Durch Vertauschen der Begriffe innen und au§en beim Ansetzen der gleichseitigen Dreiecke ergibt sich eine zweite Lšsung (Abb. 5).
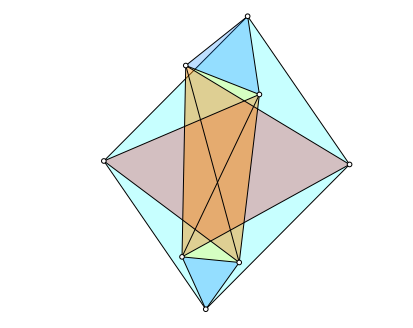
Abb. 5: Zweite Lšsung
Die beiden Lšsungen haben dieselben SeitenlŠngen, aber unterschiedliche Winkel.
Website
Hans
Walser: Varignon
http://www.walser-h-m.ch/hans/Miniaturen/V/Varignon2/Varignon2.htm