Hans Walser, [20100701a]
Verallgemeinerung der Binomialkoeffizienten
1
Worum geht es?
Wir verallgemeinern die
fŸr die Binomialkoeffizienten gŸltige Rekursionsformel 
zu
mit den Randwerten 
, 
und 
und untersuchen
einige Analoga von lieb gewonnenen Eigenschaften des Pascal-Dreieckes der
Binomialkoeffizienten.
2
Schreibweisen und Darstellungen
Wir verwenden je nach
Bedarf die symmetrische Darstellung der Zahlendreiecke oder die Darstellung mit
Linksanschlag, in welcher die Binomialkoeffizienten als Elemente einer (unendlich
gro§en) unteren Dreiecksmatrix erscheinen.
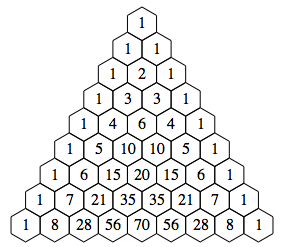
Pascal-Dreieck in
symmetrischer Darstellung
Die Matrix des Pascal-Dreieckes
der Binomialkoeffizienten bezeichnen wir mit P. Die Matrix mit den Elementen 
bezeichnen wir
mit 
. Es ist 
.
Pascal-Dreiecksmatrix
3
Beispiele
3.1
p = 2 und q = 1
Mit der Rekursion 
erhalten wir:
Bemerkungen:
Matrizen: Es ist 
.
Geometrie: Die Matrix 
hat einen
geometrischen Querbezug: In der Zeile n
(Nummerierung beginnt mit 0) finden wir die Anzahl der Bauelemente des n-dimensionalen WŸrfels. So hat etwa der
dreidimensionale WŸrfel 8 Ecken, 12 Kanten, 6 Quadrate (als SeitenflŠchen) und
einen 3d-WŸrfel (sich selber). Der vierdimensionale WŸrfel hat 16 Ecken, 32
Kanten, 24 Quadrate, 8 3d-WŸrfel (als Seitenhyperebenen) und einen 4d-WŸrfel.
Fibonacci: Wenn wir die
Zahlen auf Geraden mit der Steigung 1 addieren, ergibt sich die Zahlenfolge: 1,
2, 5, 12, 29, 70, 169, É . Dies ist eine Folge mit der Rekursion:
Wir haben also eine
verallgemeinerte Fibonacci-Folge.
Zeilensumme: Die
Dreiecksdarstellung ist, was die Zahlen betrifft, asymmetrisch:
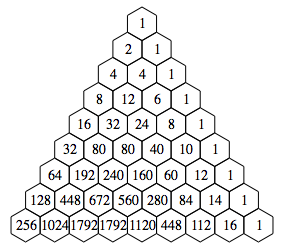
Dreiecksdarstellung
Die Zeilensummen sind
der Reihe nach 1, 3, 9, 27, 81, ..., also die Potenzen von 3.
Zahlen modulo m: Mit Ausnahme der DachschrŠge rechts sind alle
gerade. Das EinfŠrben modulo 2 bringt also nicht viel.
Gerade und ungerade
FŸr das EinfŠrben
modulo 3 ergibt sich:
Drei Farben
Noch modulo 5:
FŸnf Farben
3.2
p = 1 und q = 2
Mit der Rekursion 
erhalten wir
eine Dreiecksdarstellung, welche spiegelbildlich zum Fall 
ist.
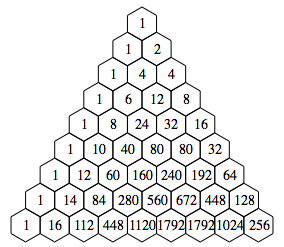
Dreiecksdarstellung
Matrizen: Um einen Link
mit der Matrix P zu finden, mŸssen wir
etwas ausholen. FŸr 
ergibt sich eine
Diagonalmatrix mit den Potenzen zur Basis 2 in der Diagonalen.
Es ist 
(Reihenfolge
wesentlich!)
3.3
p = 2, q = 3
FŠrbung modulo 5.
FŸnf Farben
4
Allgemein
Wir erhalten die
Matrix:
Es ist also:
FŸr die Zeilensumme
erhalten wir daher 
.
Matrizen: Es ist 
, 
und allgemein:
Diese Formel ist
merkwŸrdig asymmetrisch.
Fibonacci: Wenn wir die
Zahlen auf Geraden mit der Steigung 1 addieren, ergibt sich die Folge:
Wir erhalten eine
verallgemeinerte Fibonacci-Folge mit den Startwerten 
, 
und der Rekursion:
